2020牛客暑期多校训练营（第三场）D-Points Construction Problem——构造

D-Points Construction Problem

思路

第一点：千万不要考虑矩阵，千万不要考虑矩阵，千万不要考虑矩阵。因为完全可以是两个三个矩阵和几条链组成，这实在过于难考虑

这道题最难以考虑的地方就是矩阵的构造。这里给出一个思路去解决这个问题。
当然可能这个方法不是最正确的，但是结果是最优（毕竟AC了）

计算缺失边数

这个应该相对简单，即公式 (n * 4 - m) / 2 的结果

类矩阵结构

这里我们仅考虑非单链的结构，即可以出现矩阵的结构，即 $缺失边数 \geq 4$的情况

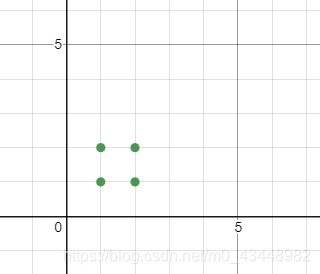
我们首先给出一个矩阵的核心部分，暂时称其为“核”

这个核有一个特性：4个点能够增加4条边，记作： $4 \rightarrow 4$

这是一个矩阵的基础，而且一个矩阵仅需要一个核。

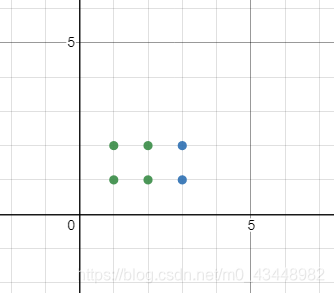
接下来最贪心的方法就是放下这样两个蓝色的点

这个结构能够实现用2个点增加3条边，记作： $2 \rightarrow 3$

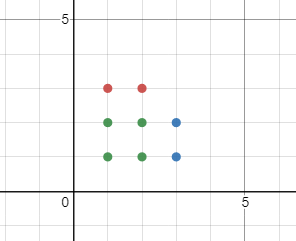
同样，我们也可以在上面放下这样的结构

同样被记作： $2 \rightarrow 3$

值得注意的是：核结构 $4 \rightarrow 4$ 是所有类矩阵结构的前提，但是由于其产生的连边数量非常少，所以尽可能的减少其使用，即整个图结构仅使用一次 $4 \rightarrow 4$。而 $2 \rightarrow 3$ 则没有次数限制，可以向上也可以向右

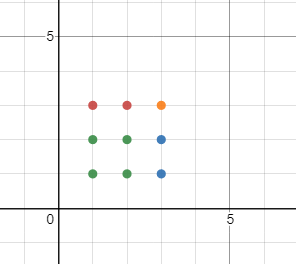
在上图的基础上，我们还可以提出一个结构：

这个橙色的点非常的巧妙，其实现了一个点新增了两条边，记作 $1 \rightarrow 2$

很明显，$1 \rightarrow 2$ 结构是最优的，结构越多则越能用较少的点来实现缺失的边的需求。所以我们需要尽可能的增加 $1 \rightarrow 2$ 的结构

但是，此结构有数量限制，其数量受到 $2 \rightarrow 3$ 的数量限制。

再考虑到矩阵的结构能够带来更多的 $1 \rightarrow 2$ 结构，所以我们选择采用如下的贪心策略

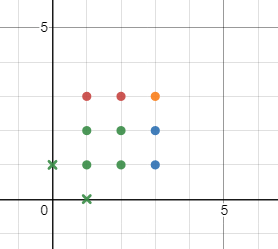
1. 先放一个$2*2$的矩阵
2. 向上/右扩展
3. 用 $1 \rightarrow 2$ 结构填充矩阵
4. 向右/上扩展
5. 用 $1 \rightarrow 2$ 结构填充矩阵
6. 重复 $2-6$ 直到缺失边全部被满足
7. 如果使用的点数超出提供的，则无解，否则将多余的点数放在遥远的天边，然后输出

剩余不满足结构

由于上述策略可能会出现遗留下 $1至2$ 条缺失边，则我们可以把点放在矩阵的左下角，即图中的×

则可以满足一条缺失边或者两条缺失边的要求

AC code

#include <bits/stdc++.h>

using namespace std;

bool flag[60][60];

void print(int n) {
    if (n < 0) {
        cout << "No" << endl;
        return;
    }
    cout << "Yes" << endl;
    while (n--)
        cout << n * 100 << " " << n * 100 << endl;
    for (int i = 0; i < 60; ++i)
        for (int j = 0; j < 60; ++j)
            if (flag[i][j])
                cout << i + 1 << " " << j + 1 << endl;
}

void solve() {
    int T;
    cin >> T;
    for (int ts = 0; ts < T; ++ts) {
        int n, m;
        cin >> n >> m;
        int target = (n * 4 - m) / 2;
        if ((n * 4 - m) & 1) {
            n = -1;
            print(n);
            continue;
        }
        memset(flag, 0, sizeof(flag));

        if (target < 4) {
            int x = 2;
            flag[1][1] = true;
            n--;

            while (target && n >= 0) {
                flag[x][1] = true;
                x++;
                target--;
                n--;
            }
            print(n);
            continue;
        }
        flag[1][1] = flag[1][2] = flag[2][1] = flag[2][2] = true;
        n -= 4;
        target -= 4;

        int l = 3, r = 3;
        while (target > 2) {
            // 右扩展
            flag[1][l] = true;
            flag[2][l] = true;
            l++;
            target -= 3;
            n -= 2;

            int len = 3;
            while (len < r && target > 1) {
                flag[len][l - 1] = true;
                target -= 2;
                n--;
                len++;
            }

            if (target > 2) {
                // 上扩展
                flag[r][1] = true;
                flag[r][2] = true;
                r++;
                target -= 3;
                n -= 2;

                len = 3;
                while (len < l && target > 1) {
                    flag[r - 1][len] = true;
                    target -= 2;
                    n--;
                    len++;
                }
            }
        }

        if (target == 2) {
            n -= 2;
            flag[0][1] = true;
            flag[1][0] = true;
        } else if (target == 1) {
            n -= 1;
            flag[0][1] = true;
        }
        print(n);
    }
}

signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
#ifdef ACM_LOCAL
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
    int test_index_for_debug = 1;
    char acm_local_for_debug;
    while (cin >> acm_local_for_debug) {
        if (acm_local_for_debug == '$') exit(0);
        cin.putback(acm_local_for_debug);
        if (test_index_for_debug > 20) {
            throw runtime_error("Check the stdin!!!");
        }
        auto start_clock_for_debug = clock();
        solve();
        auto end_clock_for_debug = clock();
        cout << "Test " << test_index_for_debug << " successful" << endl;
        cerr << "Test " << test_index_for_debug++ << " Run Time: "
             << double(end_clock_for_debug - start_clock_for_debug) / CLOCKS_PER_SEC << "s" << endl;
        cout << "--------------------------------------------------" << endl;
    }
#else
    solve();
#endif
    return 0;
}