计算机图形学
相关概念
分辨率
- 屏幕分辨率:用水平和垂直方向所能显示光点数总和的乘积表示
- 显示分辨率:用水平和垂直方向所能显示像素点总和的乘积表示
- 存储分辨率:指帧缓存区域的大小
帧缓存计算
$水平分辨率 垂直分辨率 每个像素所占用的字节$
图的表示和数据结构
- 复杂的图形通常被看作是由一些基本图形元素(图元)构成的。基本二维图元包括点、直线、圆弧、多边形、字体符号和位图等
- 图元通常是指不可再分的独立的图形实体。一个图元中的所有像素点、直线、顶点等是作为一个整体存在的,不再细分为独立的图元。
基本图形生成算法
直线生成算法
数值微分法
定义
$$\epsilon = \frac{1}{max(|\Delta x|, |\Delta y|)}$$则递推公式为
$$ \left\{ \begin{aligned} x' = Math.round(x + \epsilon \cdot \Delta x) \\ y' = Math.round(y + \epsilon \cdot \Delta y) \end{aligned} \right. $$逐点比较法
略
Bresenham 直线算法
假定 $\Delta x > \Delta y$
- 计算得到 $\Delta x = (x_1 - x_0), \Delta y = (y_1 - y_0)$
- 定义 $x = x_0, d = - \Delta x, y = y_0$
- 绘制点 $(x_0, y_0)$
- 将 $x = x + 1$
- 将 $d = d + 2 \cdot \Delta y$
- 若 $d > 0$ 则 $d = d - 2 \cdot \Delta x, y = y + 1$
- 绘制点 $(x, y)$
- 若 $x \neq x_1$ 则跳到第三步
二次曲线生成算法
Bresenham 整圆
按照八分法画圆,先绘制 $\frac{\pi}{2} 至 \frac{\pi}{4}$ 的圆,即下图的 $1b$ 区域
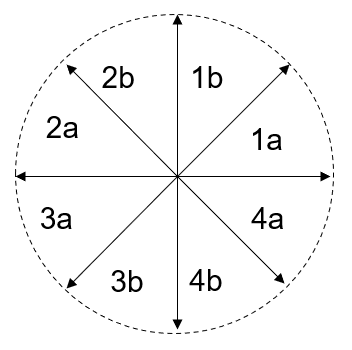
定义圆的半径 $R$,则
- 定义 $d = 1 - R, x = 0, y = R$
- 绘制点 $(x, y), (x, -y), (-x, y), (-x, -y), (y, x), (y, -x), (-y, x), (-y, -x)$
- $x = x + 1$
- 若 $d < 0$ 则 $d = d + 2x + 3$ 反之 $d = d + 2(x - y) + 5, y = y - 1$
- 若 $x < y$ 则返回步骤 2,否则结束
区域填充算法
种子填充算法
在区域内部找到一个像素,通过在这个像素的基础上,对邻接的像素进行搜索,并将邻接的像素作为下一个种子
扫描线种子填充算法
给定的种子点开始,填充当前扫描线上种子点所在的区间,然后确定与这一区间相邻上下两条扫描线上需要填充的区间,在这些区间上取最左侧或最右侧的一个点作为新的种子点。不断重复以上过程,直至所有区间都被处理完
- 初始化一个栈用来存放种子点
- 将初始的种子放入栈中
- 若栈为空,则结束算法
- 取出栈上的第一个点,作为当前种子
- 从当前种子出发,向左右两边延伸,直到遇到边界
- 从左往右扫描这条扫描线相邻的 $y - 1$ 和 $y + 1$ 的像素,若不是边界,则将其中所有相邻线段的最右边的像素放入栈中
- 回到第三步
射线法
从外部点出发,沿任意方向发射射线,若射线与多边形的交点个数为奇数,则为内部,否则为外部
弧长法
略
有效边表算法
考虑对于每一条直线 $y = kx + b$,当 $y’ = y + 1$ 时, $x’ = x + \frac{1}{k}$。所以求交点时,若已知一个交点 $(x, y)$,则可以通过上述公式推导出下一个交点为 $(x + \frac{1}{k}, y + 1)$
所以依照上述结论,得出如下的操作(以下图为例)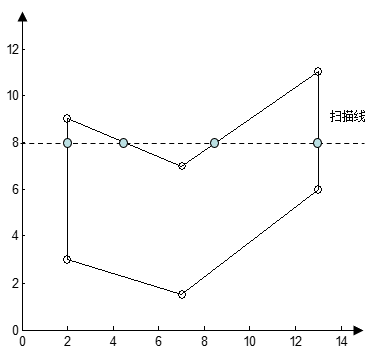
- 构建一个长度等于几何图形的最大高度的表格
- 将几何图形的每一条边的最低点的 $x, y_{max}, \frac{1}{k}$ 保存进入对应的 $y_{min}$ 表格中,(这三个值的顺序可以任意交换,例如下面的所有图中的数据顺序为 $y_{max}, x, \frac{1}{k}$ ),对于每一个单元,按照 $x$ 进行从小到大排序,若 $x$ 相同,则按照 $\frac{1}{k}$ 从小到大排序。所以可以得到下面的表格
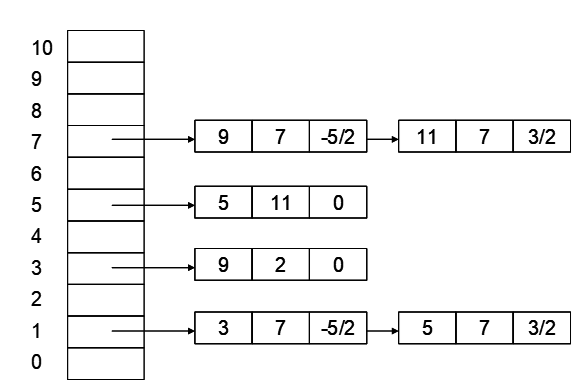
- 从最小的 $y$ 开始,不断增大 $y$,根据上一次的 $y$,计算 $y’ = y + 1$ 时,每一个元素对应的 $x’ = x + \frac{1}{k}$ ,对于当前的 $y$ 从第一个节点遍历到最后一个节点,若经过的节点数为奇数,则将这块区域内都进行染色,然后移除所有 $y = y_{max}$ 的数据,可以得到下图
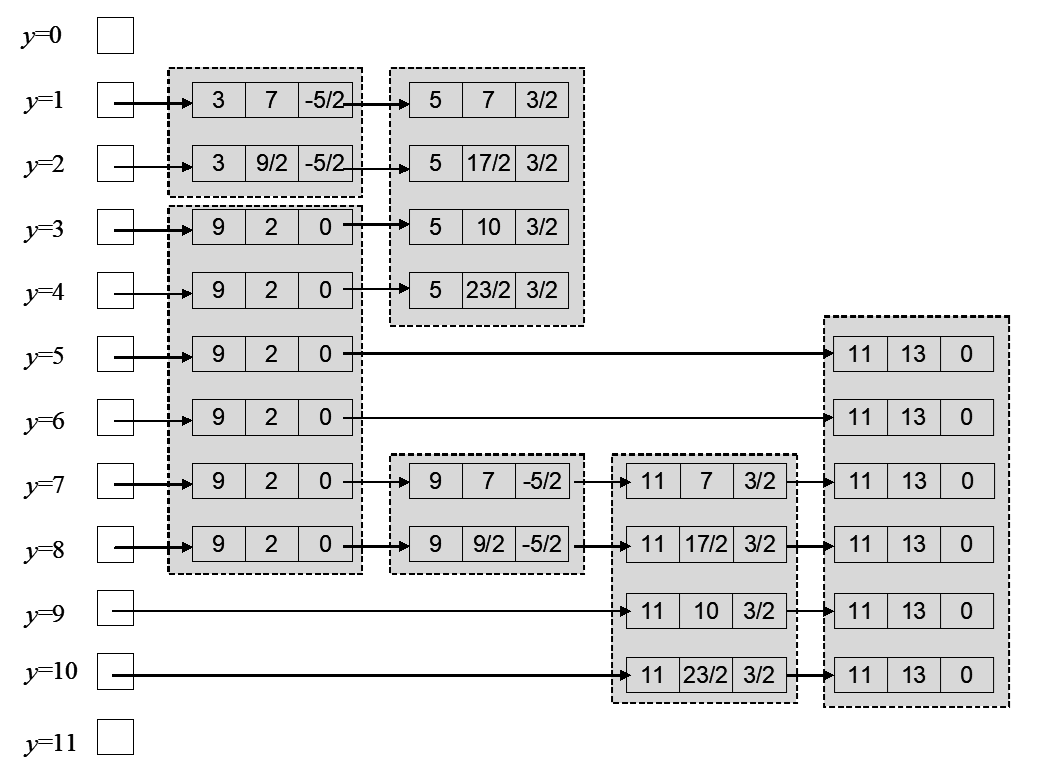
字符
略
反走样技术
形式
- 倾斜的直线和区域的边界呈阶梯状、锯齿状
- 图像细节失真,由于离散像素的四舍五入导致了本应均匀的纹理图案变得不均匀显示
- 很细小的线和点由于分辨率低而不能被显示出来
解决方法
- 超采样:以高于物理设备的分辨率完成光栅化,然后再回归到物理设备的分辨率
- 计算线段跨越的面积,确定颜色值
二维观察
使用齐次坐标表示一个点的坐标
$$ \left( \begin{matrix} x & y \end{matrix} \right) \rightarrow \left( \begin{matrix} x & y & 1 \end{matrix} \right) $$为什么使用齐次坐标系:使图形变换转化为表示图形的点集矩阵与某一变换矩阵相乘,可以借助计算机的高速运算
几何变换
平移
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ T_x & T_y & 1 \end{matrix} \right] = \left[ \begin{matrix} x + T_x & y + T_y & 1 \end{matrix} \right] $$比例缩放
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} xS_x & yS_y & 1 \end{matrix} \right] $$或
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & S \end{matrix} \right] = \left[ \begin{matrix} \frac{x}{S} & \frac{y}{S} & 1 \end{matrix} \right] $$旋转
关于原点进行逆时针旋转
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} xcos(\theta) - ysin(\theta) & xsin(\theta) + ycos(\theta) & 1 \end{matrix} \right] $$关于原点进行顺时针旋转
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} xcos(\theta) + ysin(\theta) & -xsin(\theta) + ycos(\theta) & 1 \end{matrix} \right] $$对称变换
关于 x 轴对称
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} x & -y & 1 \end{matrix} \right] $$关于 y 轴对称
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} -x & y & 1 \end{matrix} \right] $$关于 原点 轴对称
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} -x & -y & 1 \end{matrix} \right] $$关于 $y = x$ 轴对称
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} y & x & 1 \end{matrix} \right] $$关于 $y = -x$ 轴对称
$$ \left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right] \left[ \begin{matrix} 0 & -1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} -y & -x & 1 \end{matrix} \right] $$错切变换
略
二维图形几何变换
定义
$$\mathbf P = \left[ \begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \dots \\ x_n & y_n & 1 \end{matrix} \right] $$为这个二维多边形的所有顶点的坐标矩阵,此时再乘上变换矩阵,得到最终结果
复合变换
相对任意参考点的二维变换
先通过平移变换将参考点移动至原点,然后进行变换,然后再重做平移变换进行撤销一开始的变换
相对任意方向的二维变换
先通过旋转变换将参考点移动至原点,然后进行变换,然后再重做旋转变换进行撤销一开始的变换
二维观察
略
裁剪
点的裁剪
对于点 $P(x, y)$,若满足 $x_{wl} \leq x \leq x_{wr}$ 且 $y_{wb} \leq y \leq y_{wt}$ 则在窗口内,否则在窗口外
直线的裁剪
Cohen-Sutherland 算法
对一条直线的两个顶点进行编码
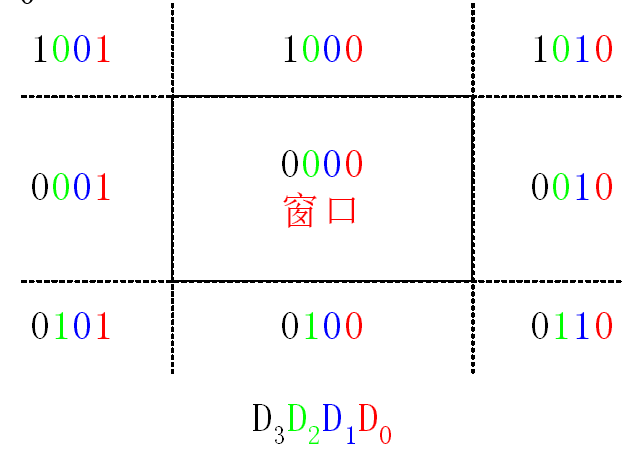
如图,若 $x < x_l$ 则 $D_0 = 1$。若 $x > x_r$ 则 $D_1 = 1$。若 $y < y_b$ 则 $D_2 = 1$。若 $y > y_t$ 则 $D_3 = 1$
若两个点 $p_1, p_2$ 的编码 $code_1, code_2$ 满足 $code_1 | code_2 = 0$ 则这条直线就在窗口内,若 $code_1 \& code_2 \neq 0$ 则这条直线可以直接抛弃掉。其他情况只需要求出这条直线和四条边的交点即可
所以可以得到如下的流程
- 输入点 $p_1, p_2$
- 对这两个点进行编码,结果为 $code_1, code_2$
- 若 $code_1 = 0$ 且 $code_2 = 0$ 则绘制直线 $p_1, p_2$,然后退出
- 若 $code_1 \& code_2 \neq 0$ 则直接退出
- 若 $code_1 = 0$ 则交换 $p_1, p_2$,同时交换 $code_1, code_2$
- 若 $code_1 的 D_0 \neq 0$ 则计算直线和 $x = x_l$ 的交点,并将其赋值给 $p_1$,返回第二步
- 若 $code_1 的 D_1 \neq 0$ 则计算直线和 $x = x_r$ 的交点,并将其赋值给 $p_1$,返回第二步
- 若 $code_1 的 D_2 \neq 0$ 则计算直线和 $y = y_b$ 的交点,并将其赋值给 $p_1$,返回第二步
- 若 $code_1 的 D_3 \neq 0$ 则计算直线和 $y = y_t$ 的交点,并将其赋值给 $p_1$,返回第二步
计算交点时,可以借用比例的方式计算,例如计算与 $x = x_l$ 的交点时,可以得到
$$ \left\{ \begin{aligned} x' & = & x_l \\ y' & = & y_1 + (y_2 - y_1) \times (x_l - x_1) / (x_2 - x_1) \end{aligned} \right. $$中点分割算法
使用了和 Cohen-Sutherland 完全相同的编码方式,但在求解交点时略有不同。此方法包含一个“求出距离一个点最远的,且在窗口内的点”。所以分别对 $p_1, p_2$ 进行一次求解,并代替掉对方(即对于 $p_1$ 求解的答案,代替掉 $p_2$)即可,以下方法的是对 $p_1$ 进行求解的操作,对 $p_2$ 求解时,交换两个值即可
- 若 $code_2 = 0$ 则返回 $p_2$
- 求出 $p_1$ 和 $p_2$ 的中点 $p_3$
- 若 $code_3 = 0$ 则用 $p_3$ 代替 $p_1$(仅算法内代替)
- 若 $code_3 \neq 0$ 则若 $code_1 \& code_3$ 则用 $p_3$ 代替 $p_1$,反之,则用 $p_3$ 代替 $p_2$,回到第二步
Liang-Barsky 算法
- 计算 $$ \left\{ \begin{aligned} p_1 & = & -(x_2 - x_1) \\ p_2 & = & x_2 - x_1 \\ p_3 & = & -(y_2 - y_1) \\ p_4 & = & y_2 - y_1 \\ q_1 & = & x_1 - x_l \\ q_2 & = & x_r - x_1 \\ q_3 & = & y_1 - y_b \\ q_4 & = & y_t - y_1 \end{aligned} \right. $$
- 若满足 $p1 = 0 \ AND \ (q1 < 0 \ OR \ q2 < 0)$ 则直线不在窗口内
- 若满足 $p3 = 0 \ AND \ (q3 < 0 \ OR \ q4 < 0)$ 则直线不在窗口内
- 准备两个数组 $pos, neg$,将 $1$ 加入到数组 $pos$ 中,将 $0$ 加入到数组 $neg$ 中
- 若 $p1 = 0$ 则跳到第七步
- 若 $p1 < 0$ 则将 $r1$ 放入 $neg$,把 $r2$ 放入 $pos$。反之,则将 $r1$ 放入 $pos$,把 $r2$ 放入 $neg$($r1 = q1 / p1$,$r2 = q2 / p2$,下同)
- 若 $p3 = 0$ 则跳到第九步
- 若 $p3 < 0$ 则将 $r3$ 放入 $neg$,把 $r4$ 放入 $pos$。反之,则将 $r3$ 放入 $pos$,把 $r4$ 放入 $neg$
- 定义 $rn1$ 为 $neg$ 中的最大值,$rn2$ 为 $pos$ 中的最小值
- 若 $rn1 > rn2$ 则直线不在窗口内
- 得到交点为 $(x1 + p2 \times rn1, y1 + p4 \times rn1), (x1 + p2 \times rn2, y1 + p4 \times rn2)$
多边形的裁剪
Sutherland-Hodgeman 算法
适合凸多边形,对于凹多边形则需要先分解为多个凸多边形
对于窗口的所有边界,进行一轮裁剪,裁剪对象是多边形的所有的边。
对于一个多边形,可以认为是一系列的顶点集合,顶点之间的连线即为一个多边形。沿着顶点的连线,进行如下的裁剪操作
- 若从窗口内到窗口外,则输出交点 $I$
- 若从窗口外到窗口内,则输出交点 $I$ 和到达点 $P$
- 若从窗口内到窗口内,则输出到达点 $P$
- 若从窗口外到窗口外,则不输出
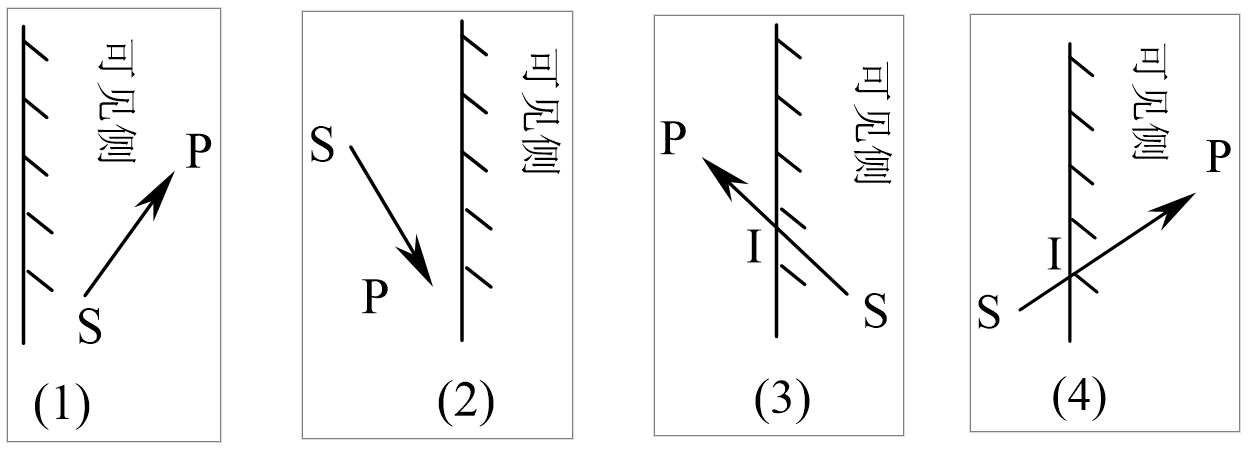
将所有输出的点连接,得到新的多边形
对于窗口的所有边界都进行一次如上的操作,即可得到最终的图像,例如下图,为左边界对此多边形进行裁剪的结果
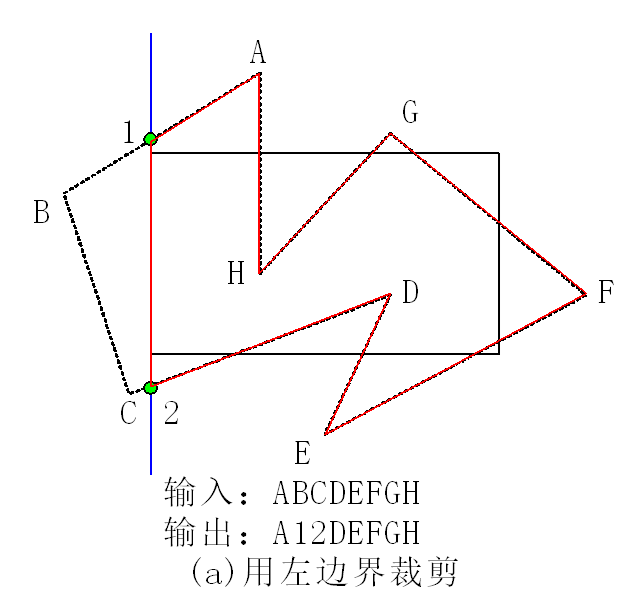
Weiler-Atherton 算法
从多边形 $P_s$ 的任意一点出发,顺时针遍历所有点
- 若出现从窗口外进入窗口内,则输出在窗口内的直线
- 若一直在窗口内,则输出直线
- 若出现从窗口内进入窗口外,则输出在窗口内的直线,并从此交点 $p_1$ 出发,顺时针的遍历窗口边界的所有点,直到找到第一个与窗口边界相交的多边形的点 $p_2$,则输出 $p_1, p_2$ 的这条路线
三维观察
三维变换
平移
$$ \left[ \begin{matrix} x' & y' & z' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & z & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ T_x & T_y & T_z & 1 \end{matrix} \right] = \left[ \begin{matrix} x + T_x & y + T_y & z + T_z & 1 \end{matrix} \right] $$缩放
旋转
将右手大拇指指向旋转轴的正方向,然后四个手指的弯曲方向即为正旋转方向
绕z轴旋转
绕x轴旋转
绕y轴旋转
三维投影
投影类型
- 透视投影
- 一点透视
- 两点透视
- 三点透视
- 正投影
- 斜投影
三维投影变换
略
曲线与曲面
概念
- 拟合:对已经存在的离散点列构造出尽可能光滑的曲线或曲面,用以直观(而忠实)地反映出实验特性、变化规律和趋势等。
- 插值:通过所有的特征点
- 逼近:不通过或部分通过特征点,并在整体上接近这些特征点
连续性条件
参数连续
- C0 连续:交点处的两条曲线段相交
- C1 连续:交点处的两条曲线段相交,且此点的一阶导函数值相同
- C2 连续:交点处的两条曲线段相交,且此点的一阶和二阶导函数都相同
几何连续
- G0 连续:交点处的两条曲线段相交
- G1 连续:交点处的两条曲线段相交,且此点的一阶导函数值成比例
- G2 连续:交点处的两条曲线段相交,且此点的一阶和二阶导函数都成比例
三次样条(二维)
对于 $n$ 个点,用 $n - 1$ 条曲线连接,对于每一条直线看,可以用一个三阶函数表示,所以得到
则对于所有的曲线,由于所有曲线必须保证 G0 连续,所以可以得到如下等式
又为了保证 G1 连续,则可以得到他们的导数相同
为了保证 G2 连续,则他们的导数的导数相同,所以还可以得到
由此,可以计算出所有的参数
Bézier 曲线
一阶导数
二阶导数
对称性
颠倒控制顶点,Bézier 曲线仍然保持,走向相反
凸包性
略
几何不变性
Bézier 曲线与坐标轴无关
G1 连续
由于一阶导数可知,若需要满足 G1 连续,则必须要满足第一条曲线的最后两个控制点和第二条曲线的开始两个控制点在同一条直线上,且保证不在同一侧,即
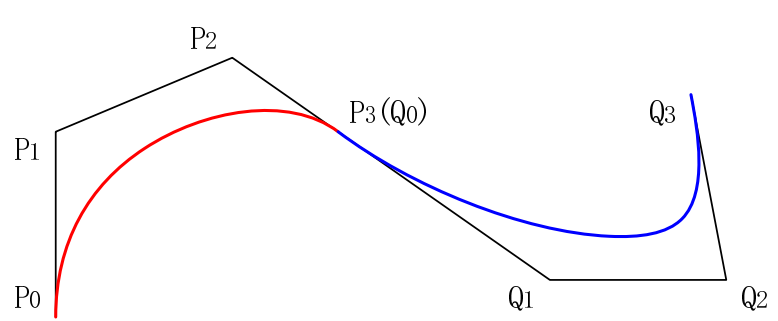
G2 连续
消隐
z-buffer
向 z 轴的负方向作为观察方向,以其 z 轴的大小作为深度值,保存每一个像素的颜色值和深度值,当此像素被再次覆盖时,若新的深度比之前保存的大,则用新的深度和颜色覆盖之前的值,否则不更换
画家算法
将物品从远到近排列,先绘制远处的图形,再由近处的图形进行覆盖
光线投射算法
对于屏幕上的每一个像素点,构造一条模拟视线的射线,由射线的交点来确定深度最大的点
光照
光照模型
用于物体表面采样点处光强度的计算
明暗处理
恒定光强的多边形绘制
取一个平面内的任意一个点的光强来表示整个平面的光强
计算量非常小,粗糙,亮度变化大,出现马赫带效应
Gouraud
根据多边形在顶点处的光强,线性插值求出平面内其他点的光强
计算量小,算法简单,出现马赫带效应,对镜面反射效果不佳
Phong
根据多边形在顶点处的法向量,线性插值求出平面内其他点的法向量
计算量大,效果好,精度高
光线跟踪算法
基于几何光学原理,模拟光的传播路径来确定反射、折射和阴影。通过“过采样”的方式,实现反走样