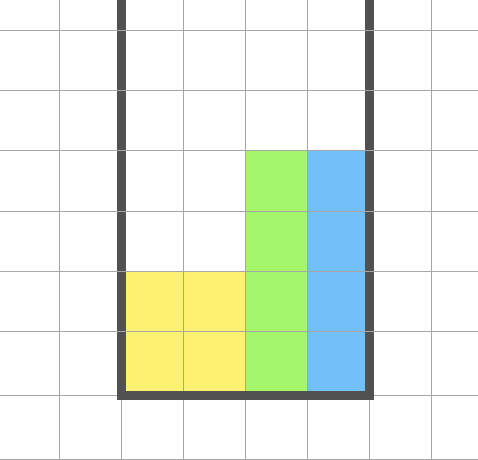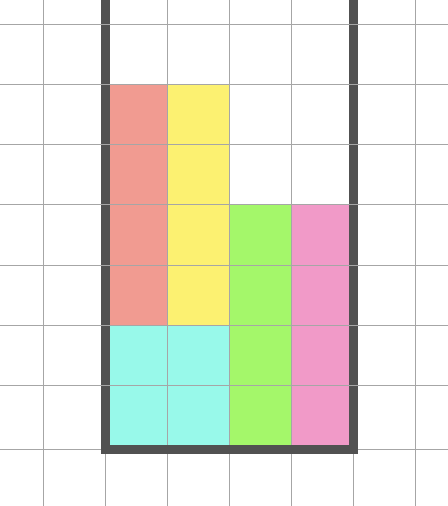2021年浙江工商大学新生赛题解

本篇中的题目顺序为预期难度顺序，并非比赛题目顺序
本篇中所有的“更好的优化”均为标准答案之外的思考，不使用此内容也可以通过题目

比赛预期情况

总共比赛人数：175 (至少通过一道题的人数，没有通过题的不计入总人数)

题目名	实际通过次数	实际通过比例	预期通过比例
chiking 的偶像	172	98.3%	100%
chiking 和珂朵莉	141	80.6%	80%
chiking 的序列 II	58	51.3%	60%
chiking 的序列 I	113	64.6%	50%
chiking 的棋盘	2	1.1%	30%
乐于助人的 chiking	24	13.7%	20%
chiking 的俄罗斯方块	0	0%	1%
chiking 和大家一起来做签到题	0	0%	1%
chiking 是一个机器人	0	0%	1%

综上来看，整个新生赛除了一道题没有达到预期的成绩，其他题目均与预期相差不大

题解

chiking 的偶像

大致题意

循环输出 \soup_god/，且总共输出的字符串长度为 $n$

思路

简单的签到题，只需要还记得有 mod 这个运算就能写出来

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
    const char *data = "\\soup_god/";
    int n;
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cout << data[i % 10];
    }
    cout << endl;
}

吐槽

我以为大家被卡在不会 mod，结果大家都卡在 \\，这就挺尴尬的

chiking 和珂朵莉

大致题意

$n$ 个物品，每个物品都有价值和所属类别，让你选择 $n - k$ 种类别的物品，使得所选出来的这些类别的物品的总价值最大

思路

也是签到题之一

在读入数据的时候统计每个类别的物品价值只和，之后排序一下，取出后 $n - k$ 个类别的价值即可

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
    int w[11] = {0};
    int m, n, k;
    cin >> m >> n >> k;
    for (int i = 0; i < m; ++i) {
        int d, s;
        cin >> d >> s;
        w[s] += d;
    }
    sort(w + 1, w + n + 1);
    int ans = 0;
    for (int i = k + 1; i <= n; ++i) ans += w[i];
    cout << ans << endl;
}

吐槽

这道题原来有一个小坑点，即物品的价值可以为负数，所以需要额外增加一个判断，但是想了想还是当签到题，不要故意恶心了，于是就删掉了。所以顺便好奇的问一下，有多少人看到题面之后去想过价值是不是可能为负数呢

chiking 的序列 II

大致题意

有一个非递减的数组，允许你进行任意次数操作，每次操作可以使得其中一个值增加 $1$，问至少需要多少次操作才能使得数组内没有相同的值

思路

因为只能进行加法运算，所以数字只会增加，由于已经排序好了数组，所以最简单的方案就是让每一个值都比前一个值要大即可

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> data(n);
    for (int i = 0; i < n; ++i) cin >> data[i];
    long long sum = 0;
    for (int i = 1; i < n; ++i) {
        int tmp = max(data[i - 1] + 1, data[i]);
        sum += tmp - data[i];
        data[i] = tmp;
    }
    cout << sum << endl;
}

chiking 的序列 I

大致题意

有一个数组，允许你进行任意次操作，每次执行操作可以将任意一个数字插入到数组到任意位置，问至少需要多少次操作才能使得数组内到每一个值满足 $a_i \leq i$，其中 $i$ 表示下标

思路

首先要让每一位的的数字小于等于其下标，那么插入的数字也不能例外。由于插入的数字可以是任意值，所以理所应当的，选择 $1$ 进行插入是最好的选择，因为无论插入何处均可以使得新插入的数字不再需要考虑

接下来是考虑插入位置的问题，在等式中 $a_i$ 是不可更新的值，所以只能想办法使得 $i$ 增大，那么最容易得到的解决方案就是将数字插入数组开头，这会使得所有原来在数组内的值的下标都增大，最大程度的满足条件

接下来考虑插入数量的问题，由于都是插入数组最前面，所以可以将等式改写为 $a_i <= i + x$，其中的 $x$ 即为需要求解的值。那么对于每一个 $i$ 都要满足这个等式，所以遍历一次数组，找出最大的需要的 $x$ 即可

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int tmp;
            cin >> tmp;
            ans = max(ans, tmp - i - 1);
        }
        cout << ans << endl;
    }
}

chiking 的棋盘

大致题意

用 $k$ 个 L 形状的方块能否平铺一个矩形方格

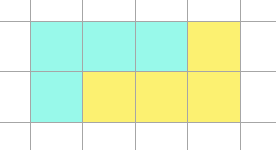
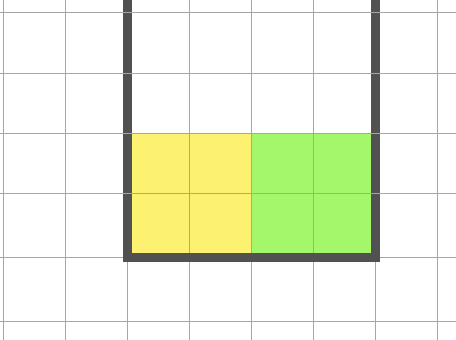
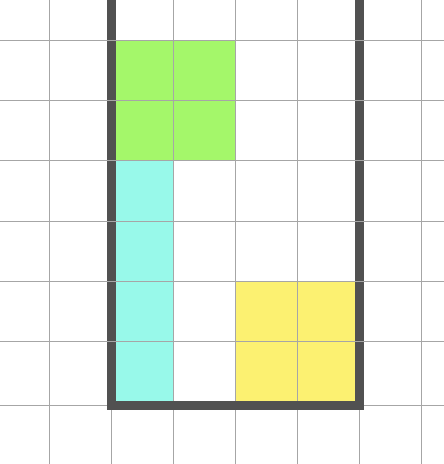
思路

我们可以用 L 形状的方块拼出如下两种最简平铺方案

2-4

3-8

这两个方案都是 $8$ 个方格的倍数，所以起码，方格总数应该是 $8$ 的倍数，即 $n \times m = 8k$

假设两边都是偶数，那么必然其中一边为 $2$ 的倍数，另外一边为 $4$ 的倍数，所以必然可以被仅靠第一种平铺方案平铺
假设一边为奇数一边是偶数，那么必然其中一边为 $8$ 的倍数，而第一种方案也可以改写为 $2 * 8$ 的方格，即只需要另外一边可以分解为 $2x + 3y$ 的形式即可，易得只要 $ \geq 2$ 的值均可

所以结论：只要满足方格数为 $8$ 的倍数，且两边都 $\geq 2$，则必定可以平铺

接下来只需要计算数量对不对就行

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
#define int long long
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, m, k;
        cin >> n >> m >> k;
        if (n > 1 && m > 1 && (n * m) % 8 == 0) {
            int cnt = (n * m / 4);
            if (cnt == k) cout << "Perfect!\n";
            else cout << "Single forever!\n";
        } else cout << "Single forever!\n";
    }
}

乐于助人的 chiking

大致题意

允许将字符串中 oo 和 u 互转，也允许将字符串的 kh 和 h 互转的前提下，计算给出的字符串数组中有几个不同的字符串

思路

由于存在转换，所以最好的办法就是统一转为一种类型，再进行比较

oo 和 u 这对规则，若我们将所有的 oo 转为 u，那么当遇到 ou 和 uo 时，会发现在此条规则下应该是相等的字符串没有相等。所以应该将所有的 u 字符转为 oo

kh 和 h 这对规则，若我们将所有的 h 转为 kh，那么就会出现 kh 还可以继续转为 kkh、kkkh、kkkkh 等，所以只能选择将 kh 转为 h。但是请注意 kkkh 这类连续的 k 的情况，可以连续多次转换

处理完成后，统计不同的字符串的数量即可

处理字符串复杂度 $O(nm) = 1e5$
统计不同字符串数量 $O(n^2m) = 1e7$

满足要求

AC Code

#include "bits/stdc++.h"

using namespace std;

char a[1010], b[2010];

void solve() {
    int n;
    cin >> n;
    vector<string> data;
    for (int i = 0; i < n; ++i) {
        cin >> a;
        int len = (int) strlen(a);
        int pos = 0;
        for (int j = 0; j < len; ++j) {
            if (a[j] == 'u') {
                b[pos++] = 'o';
                b[pos++] = 'o';
            } else if (a[j] == 'h') {
                while (pos > 0 && b[pos - 1] == 'k') pos--;
                b[pos++] = 'h';
            } else {
                b[pos++] = a[j];
            }
            b[pos] = 0;
        }
        data.emplace_back(b);
    }
    int cnt = 0;
    for (int i = 0; i < n - 1; ++i) {
        bool flag = true;
        for (int j = i + 1; j < n; ++j) {
            if (data[i] == data[j]) {
                flag = false;
                break;
            }
        }
        if (flag) cnt++;
    }
    cout << cnt + 1 << endl;
}

更好的优化

实际上，这里需要比较的是字符串是否相同，所以可以使用字符串 hash 来解决，这样，复杂度将会降低至 $O(nm)$。当然，字符串 hash 存在一定的可能错误的隐患，但是可以通过增加多组 hash 来解决

Better Code

#include "bits/stdc++.h"

using namespace std;

char a[1010], b[2010];

void solve() {
    int n;
    cin >> n;
    set<long long> hashCode;
    for (int i = 0; i < n; ++i) {
        cin >> a;
        int len = (int) strlen(a);
        int pos = 0;
        for (int j = 0; j < len; ++j) {
            if (a[j] == 'u') {
                b[pos++] = 'o';
                b[pos++] = 'o';
            } else if (a[j] == 'h') {
                while (pos > 0 && b[pos - 1] == 'k') pos--;
                b[pos++] = 'h';
            } else {
                b[pos++] = a[j];
            }
        }
        long long code = 0;
        const long long p = 131, m = 1e9+7;
        for (int j = 0; j < pos; ++j) {
            code *= p;
            code %= m;
            code += b[j];
            code %= m;
        }
        hashCode.insert(code);
    }
    cout << hashCode.size() << endl;
}

chiking 的俄罗斯方块

大致题意

宽度为 4 的俄罗斯方块游戏，仅有两种方块：$2 \times 2$ 的方块和 $1 \times 4$ 的长条，在已知所有的下落顺序的情况下，求出最优的分数

思路

需要思考的东西比较多，我们先来证明一些东西，方面后面使用

实际上仅会出现 10 分和 3 分两种消方块

这个结论应该是比较简单就可以得出的，因为垂直方向上只有长度为 2 和 4 的方块，所以当我们能遇到创造出 10 分的情况，尽快消除绝对不会亏

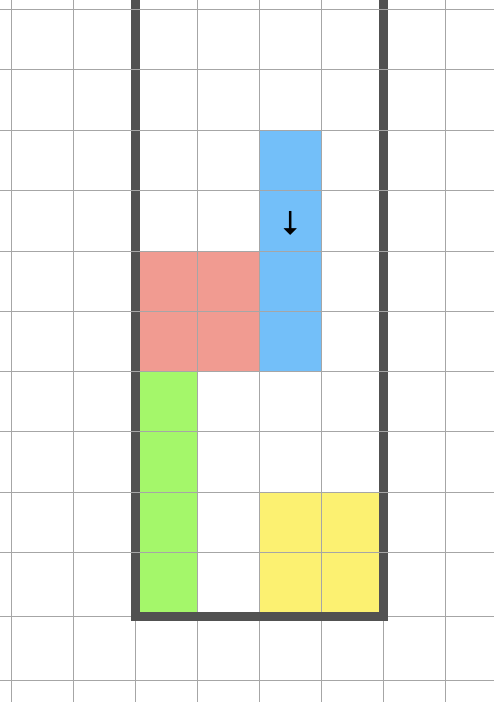
长条方块必定可以合并视为 $2 \times 4$

这个结论指的是如下的情况是不可能发生的(带箭头的蓝色方块是最后落下的)

Tetris-cannot be inserted

因为这个情况下，才会出现 $1 \times 4$ 无法插入到原来的 $1 \times 4$ 中使得变成 $2 \times 4$

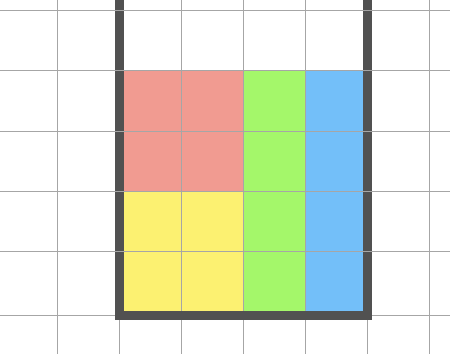
而这个情况恰好满足一个 10 分的消除情况，即下图

10-1

既然能创造 10 分，那么就没必要纠结是不是能够合并了，先变成 10 分重要，所以不存在单独一根的长条方块的情况

将 2*2 放中间一定不是好的选择

这个结论应该显而易见吧，因为放左/右边既可以与 $1 \times 4$ 消分，还可以与 $2 \times 2$ 消分，比放中间肯定更优

原来的结构不影响当前期望的分数

这句话扩展起来就是

不管之前的方块带来什么影响，若接下来 n 个方块能够创造 10 分的价值，则一定可以创造 10 分的价值，若接下来 n 个方块能创建 3 分的价值，则一定可以创造 3 分的价值

这一条暂且先不证明

所有组合如下

所有能够拿分的组合只有下面这些，其中只有前两个是 10 分，其他的均为 3 分

10-1

10-2

3-1

3-2

接下来我们可以证明上面那条的结论

之前方块带来的影响主要是由于其必须要先落下导致占用了一定的位置，使得原来可以消掉的方块没有办法继续消除

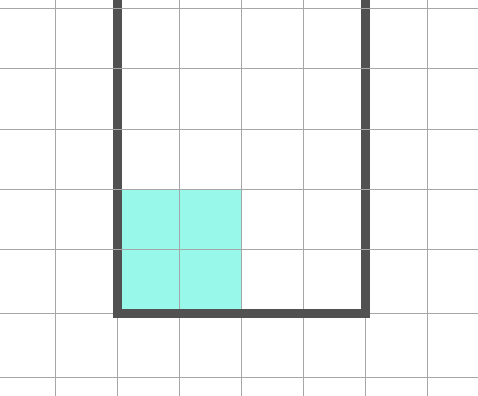
最常见的一个影响就是 $2 \times 2$ 影响，简单来说就是原来已经有一块 $2 \times 2$ 方格，此时就不一定能够做到满足上述的消分情况，如下图

例如此时，其实无法完美的满足第二种 10 分的消分情况，因为你不可能将四个 $1 \times 4$ 放在同一行中，即同时下落四个 $1 \times 4$ 的方块时，你不能仅通过这四个方块得到 10 分

但是又如何呢？

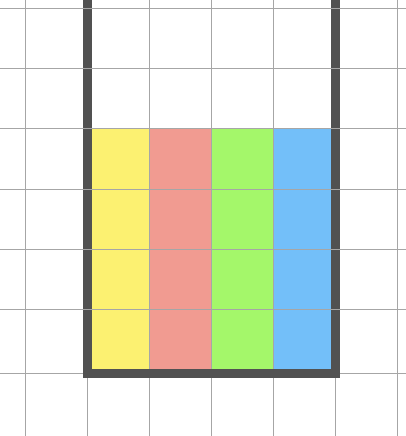
实际上我们仍然可以拿到 10 分，而且最后剩下的结果仍然是 $2 \times 2$方块，如下图所示

2-2-block-solve

这里就不再详细介绍每种情况了，供各位思考在 $2 \times 2$ 的影响下，四种得分方案是否都可以得到原来的分数且不带来新的影响

还有一种影响是 $2 \times 4$ 的，比较类似，不再详细说明了

特别的，无论在 $2 \times 2$ 还是 $2 \times 4$ 的影响下，第三种得分方案都有可能会从 3 分变成 10 分，而这虽然增加了分数，但是同时也增加了难于预料的问题，必须予以解决。有趣的是，这种新的得分方案，其实正是第一种方案，所以如果我们能够优先将所有可能的第一种方案计算完，那么此情况其实不再可能出现，那么也就可以忽略了

除了 $2 \times 2$ 还是 $2 \times 4$，还有更多的可能，例如更高的 $2 \times 8$ 等等，但实际上是类似的，也就不再需要证明

当然还有更加离谱的影响，例如 $1 \times 4$ 影响，明显，这个影响确实真的影响到得分了，因为第四种得分方案压根不可能得分了，如下图

1-4-block-solve

但是，注意题目中说的 $1 \times 4$ 一定是偶数个，所以之后必定有一个 $1 \times 4$，那么就回到了开头的那个结论的情况，这里又可以拿到 10 分了

穿插组合并无影响

简单来说就是两个结构需要的方块穿插起来，并不会影响最终的得分，这里就不再详细介绍

当你证明完成后接下来就是模拟讨论所有情况即可

注意第一种 10 分，其要求最后一个落下的必须是 $1 \times 4$ 的长条即可，剩下的，统计数量就行

AC Code

#include "bits/stdc++.h"

using namespace std;

void solve() {
    int n;
    cin >> n;
    int tot0 = 0, cnt0 = 0, cnt1 = 0, ans = 0;
    for (int i = 0; i < n; ++i) {
        int tmp;
        cin >> tmp;
        if (tmp == 1) {
            cnt1++;
            if (cnt1 >= 2 && cnt0 >= 2) {
                cnt1 -= 2;
                cnt0 -= 2;
                ans += 10;
            }
        } else {
            tot0++;
            cnt0++;
        }
    }
    ans += (cnt1 / 4) * 10;
    cnt1 &= 2;
    if (tot0 >= 2) {
        ans += (cnt0 + cnt1) / 2 * 3;
    } else if (cnt0 && cnt1) {
        ans += 3;
    }
    cout << ans << endl;
}

chiking 和大家一起来做签到题

大致题意

给定一个 n，允许使用加减乘除和任意括号，找出有多少种不同的四个数字，使得这四个数字能够运算出 n，且运算过程中一定出现了小数，罗列所有的可能的四个数字的组合

思路

其实就是一道暴力题

算一下复杂度，$13^4/2 \times 4! \times 2 \times 3^6 = 499,703,256$

解释一下，罗列每个位置的每个可能，为 $\rightarrow 13^4 / 2$ （避免重复，遍历过程保证前一个值不大于当前值）

排列数组 $\rightarrow 4!$

总共有两种括号方式 $((A @ B) @ C) @ D$ 和 $(A @ B) @ (C @ D)$（$ABCD$ 为数字，$@$ 为运算符号），所以 $\rightarrow 2$

枚举所有的运算符号 $\rightarrow 3^6$（6 种运算分别为 $A + B, A - B, B - A, A \times B, A \div B, B \div A$）

做一下剪枝，很容易提前放弃掉部分方案，复杂度还可以降低

所以直接暴力就行

但是，如何优雅的暴力呢？

AC code

#include "bits/stdc++.h"

using namespace std;

const double eps = 1e-6;


void solve() {

    int m;
    set<int> ans;
    int curValue[4];
    cin >> m;

    auto isM = [&](double cur) { return abs(cur - m) < eps; };
    auto isDouble = [&](double cur) { return abs(cur - int(cur + eps)) > eps; };

    auto add = [](double a, double b) { return a + b; };
    auto sub1 = [](double a, double b) { return a - b; };
    auto sub2 = [](double a, double b) { return b - a; };
    auto times = [](double a, double b) { return a * b; };
    auto div1 = [](double a, double b) { return a / b; };
    auto div2 = [](double a, double b) { return b / a; };

    function<double(double, double)> arr[6] = {add, sub1, sub2, times, div1, div2};

    auto cal = [&]() {
        bool reach = false, hasNoDouble = false;
        do {

            function<bool(double, int, bool)> dfs1 = [&](double cur, int deep, bool hasDouble) {
                if (deep == 4) {
                    if (isM(cur)) {
                        reach = true;
                        if (!hasDouble) {
                            hasNoDouble = true;
                            return false;
                        }
                    }
                    return true;
                }

                return all_of(arr, arr + 6, [&](function<double(double, double)> &func) {
                    double nxt = func(cur, curValue[deep]);
                    return dfs1(nxt, deep + 1, hasDouble || isDouble(nxt));
                });
            };
            function<bool()> dfs2 = [&]() {
                for (auto &i: arr) {
                    for (auto &j: arr) {
                        double l = i(curValue[0], curValue[1]);
                        double r = j(curValue[2], curValue[3]);
                        for (auto &k: arr) {
                            double t = k(l, r);
                            if (isM(t)) {
                                reach = true;
                                if (!isDouble(l) && !isDouble(r)) {
                                    hasNoDouble = true;
                                    return false;
                                }
                            }
                        }
                    }
                }
                return true;
            };

            dfs1(curValue[0], 1, false);
            dfs2();

        } while (next_permutation(curValue, curValue + 4));

        if (reach && !hasNoDouble) {
            // 四个小于 16 的 int 数字，可以按位压缩到一个 int 中
            int t = 0;
            for (auto &item: curValue) {
                t <<= 4;
                t += item;
            }
            ans.insert(t);
        }
    };

    // 暴力枚举没有必要一定要用 dfs，实际上 for 也可以，甚至更快，因为减少了出入栈的耗时
    for (int i = 0; i < 13; ++i) {
        curValue[0] = i + 1;
        for (int j = i; j < 13; ++j) {
            curValue[1] = j + 1;
            for (int k = j; k < 13; ++k) {
                curValue[2] = k + 1;
                for (int l = k; l < 13; ++l) {
                    curValue[3] = l + 1;
                    cal();
                }
            }
        }
    }

    cout << ans.size() << endl;
    for (auto &item: ans) {
        int cur = item;
        for (int i = 3; i >= 0; --i) {
            curValue[i] = cur % 16;
            cur >>= 4;
        }
        for (int i = 0; i < 4; ++i)
            cout << curValue[i] << " \n"[i == 3];
    }
}

chiking 是一个机器人

大致题意

有一个地图，有障碍物，三种不同的机器，一个只能下，一个只能右，最后那个可以下右移动，询问 q 次某种机器能否从起始点到终点

思路

考虑前两种机器，其实很好解决，以第一种机器举例，我将整个地图的第一行加到第二行，此时的第二行加到第三行，如此操作后，每个点上保存的是此点的正上方有多少个墙，称其为“前缀墙”。若起点和终点的点的“前缀墙”数量相同，则就可以到达，否则中间必定存在墙

第二种机器就不再过多介绍了

第三种机器则比较难做，考虑一种 dp 的可能：若这个点不是墙，则可以到达这个点的所有点，是能够到达这个点上方点的所有点和能够到达这个点左边的所有点的并集。用公式描述一下就是

$\begin{equation} dp[i][j] = \begin{cases} dp[i][j - 1] \cup dp[i - 1][j] \cup \{(i, j)\}, & \text{如果当前节点可达 } \\ 空集合, & \text{如果当前节点不可达 } \end{cases} \end{equation}$ {% raw %}

如此计算我们可以得到第一份代码

#include "bits/stdc++.h"

using namespace std;

struct Node {
    int x1, y1, x2, y2, i;

    bool operator<(const Node &rhs) const {
        return x2 < rhs.x2;
    }
};

void solve() {
    const int N = 510;
    const int M = 510;

    // 读取地图
    int n, m;
    cin >> n >> m;
    vector<bitset<M>> graph(n);

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            char c;
            cin >> c;
            graph[i][j] = c == '0';
        }
    }

    // 前缀和解决 1 和 2 型号的
    vector<vector<int>> modelList[2];
    for (auto &model: modelList) {
        model.resize(n);
        for (auto &item: model)
            item.resize(m, 0);
    }

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            modelList[0][i][j] = (i != 0 ? modelList[0][i - 1][j] : 0) + !graph[i][j];
            modelList[1][i][j] = (j != 0 ? modelList[1][i][j - 1] : 0) + !graph[i][j];
        }
    }

    int q;
    cin >> q;
    vector<bool> ans(q);    // 离线计算答案
    vector<Node> query;
    query.reserve(q);

    for (int i = 0; i < q; ++i) {
        int t, x1, y1, x2, y2;
        cin >> t >> x1 >> y1 >> x2 >> y2;
        // 下标从 0 开始
        x1 -= 1;
        y1 -= 1;
        x2 -= 1;
        y2 -= 1;

        if (t == 1) ans[i] = (y1 == y2) and (x1 <= x2) and (modelList[0][x1][y1] == modelList[0][x2][y2]);
        else if (t == 2) ans[i] = (x1 == x2) and (y1 <= y2) and modelList[1][x1][y1] == modelList[1][x2][y2];
        else {
            if (x1 > x2 || y1 > y2) ans[i] = false;
            else query.push_back((Node) {x1, y1, x2, y2, i});
        }
    }

    sort(query.begin(), query.end());

    auto hashNode = [&](const int &x, const int &y) {
        return x * n + y;
    };

    vector<bitset<N * M>> dp(m);
    for (int i = 0; i < m; ++i) {
        dp[i].reset();
        dp[i][hashNode(0, i)] = graph[0][i];
    }

    int curQuery = 0;

    for (int i = 0; i < n; ++i) {
        // 离线计算每个位置哪些可以到达
        if (!graph[i][0]) dp[0].reset();
        else dp[0][hashNode(i, 0)] = true;
        for (int j = 1; j < m; ++j) {
            if (!graph[i][j]) dp[j].reset();
            else {
                dp[j][hashNode(i, j)] = true;
                dp[j] |= dp[j - 1];
            }
        }
        while (curQuery < query.size()) {
            if (query[curQuery].x2 == i) {
                ans[query[curQuery].i] = dp[query[curQuery].y2][hashNode(query[curQuery].x1, query[curQuery].y1)];
                curQuery++;
            } else break;
        }
    }

    for (int i = 0; i < q; ++i)
        cout << (ans[i] ? "yes" : "no") << endl;
}

让我们计算一下复杂度: $O(n^4) = 500^4 = 62,500,000,000$，这肯定不行，就算压位也不能通过

所以需要优化

问题出在需要计算所有的点可达问题，这就导致了计算一个节点就需要 $O(n^2)$ 的时间，非常不合理

如果试图减少一个 $n$，那么我们只能计算能否到达某一行或者某一列的值，而不能计算全部

但是考虑双向，如果我们知道出发点能够到达某个节点。而目标点可以来自同一个点，那么也同样可以说明可以到达

所以这个特殊的一行或者一列将地图分为两半，同时若询问是跨立在这一行或者这一列，则可以回答，但是对于没有跨立的如何解决？

分治

以横向为例，不断取横向中间轴作为特定行，不断计算跨此轴的询问的解，复杂度为 $O(n^3logn) = 500^3 * log(500) = 337,371,250$，似乎可行

可以得到第二份代码

#include "bits/stdc++.h"

using namespace std;

const int QUERY_LEN = 1e5 + 10;
const int NUM = 505;
const int DIV = 505;

char mp[NUM][NUM];
int n, m, ans[QUERY_LEN];
int L[NUM][NUM], U[NUM][NUM];
struct node {
    int id, x1, y1, x2, y2;
};
vector<node> queryList;
unsigned vis1[NUM][NUM][DIV], vis2[NUM][NUM][DIV];

void reset(unsigned *v) {
    memset(v, 0, sizeof(unsigned) * DIV);
}

void cpFlag(unsigned *dist, const unsigned *from) {
    memcpy(dist, from, sizeof(unsigned) * DIV);
}

void orFlag(unsigned *dist, const unsigned *from) {
    for (int i = 0; i < DIV; ++i) dist[i] |= from[i];
}

void setFlagTrue(unsigned *v, int id) {
    v[id] = 1;
}

bool andFlagAny(const unsigned *a, const unsigned *b) {
    for (int i = 0; i < DIV; ++i) if (a[i] & b[i]) return true;
    return false;
}

void dfs(int l, int r, vector<node> &q) {
    if (l > r) return;
    int mid = (l + r) >> 1;
    for (int i = mid; i >= l; i--) {
        for (int j = m; j >= 1; j--) {
            reset(vis1[i][j]);
            if (mp[i][j] == '1') continue;
            if (i == mid) setFlagTrue(vis1[i][j], j);
            else cpFlag(vis1[i][j], vis1[i + 1][j]);
            orFlag(vis1[i][j], vis1[i][j + 1]);
        }
    }
    for (int i = mid; i <= r; i++) {
        for (int j = 1; j <= m; j++) {
            reset(vis2[i][j]);
            if (mp[i][j] == '1') continue;
            if (i == mid) setFlagTrue(vis2[i][j], j);
            else cpFlag(vis2[i][j], vis2[i - 1][j]);
            orFlag(vis2[i][j], vis2[i][j - 1]);
        }
    }
    vector<node> vl, vr;
    for (auto it: q) {
        if (it.x2 < mid) vl.push_back(it);
        else if (it.x1 > mid) vr.push_back(it);
        else ans[it.id] = andFlagAny(vis1[it.x1][it.y1], vis2[it.x2][it.y2]);
    }
    dfs(l, mid - 1, vl);
    dfs(mid + 1, r, vr);
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mp[i][j];
            if (mp[i][j] == '0') L[i][j] = L[i][j - 1] + 1;
        }
    }
    for (int j = 1; j <= m; j++) {
        for (int i = 1; i <= n; i++) {
            if (mp[i][j] == '0') U[i][j] = U[i - 1][j] + 1;
        }
    }

    int q;
    cin >> q;
    for (int i = 1; i <= q; i++) {
        int op, x1, x2, y1, y2;
        cin >> op >> x1 >> y1 >> x2 >> y2;
        if (x1 > x2 || y1 > y2) {
            ans[i] = 0;
            continue;
        }
        if (op == 1) {
            if (y1 != y2 || U[x2][y2] < x2 - x1) ans[i] = 0;
            else ans[i] = 1;
        } else if (op == 2) {
            if (x1 != x2 || L[x2][y2] < y2 - y1) ans[i] = 0;
            else ans[i] = 1;
        } else {
            queryList.push_back({i, x1, y1, x2, y2});
        }
    }
    dfs(1, n, queryList);

    for (int i = 1; i <= q; i++) cout << (ans[i] ? "yes\n" : "no\n");
}

但是，还是不对，实际上是空间超限了

仔细思考，实际上我们使用了 int 来模拟一个布尔值组，非常浪费空间，可以进行压位，得到最终的代码，此时的复杂度为 $O(n^3logn / 64) = 500^3 * log(500) / 64 = 5,271,425$，

#include "bits/stdc++.h"

using namespace std;

const int QUERY_LEN = 1e5 + 10;
const int NUM = 505;
const int DIV = 8;
const int LEN = 64;
typedef unsigned long long bits;

char mp[NUM][NUM];
int n, m, ans[QUERY_LEN];
int L[NUM][NUM], U[NUM][NUM];
struct node {
    int id, x1, y1, x2, y2;
};
vector<node> queryList;
bits vis1[NUM][NUM][DIV], vis2[NUM][NUM][DIV];

void reset(bits *v) {
    memset(v, 0, sizeof(bits) * DIV);
}

void cpFlag(bits *dist, const bits *from) {
    memcpy(dist, from, sizeof(bits) * DIV);
}

void orFlag(bits *dist, const bits *from) {
    for (int i = 0; i < DIV; ++i) dist[i] |= from[i];
}

void setFlagTrue(bits *v, int id) {
    v[id / LEN] |= ((bits) 1u) << (id % LEN);
}

bool andFlagAny(const bits *a, const bits *b) {
    for (int i = 0; i < DIV; ++i) if (a[i] & b[i]) return true;
    return false;
}

void dfs(int l, int r, vector<node> &q) {
    if (l > r) return;
    int mid = (l + r) >> 1;
    for (int i = mid; i >= l; i--) {
        for (int j = m; j >= 1; j--) {
            reset(vis1[i][j]);
            if (mp[i][j] == '1') continue;
            if (i == mid) setFlagTrue(vis1[i][j], j);
            else cpFlag(vis1[i][j], vis1[i + 1][j]);
            orFlag(vis1[i][j], vis1[i][j + 1]);
        }
    }
    for (int i = mid; i <= r; i++) {
        for (int j = 1; j <= m; j++) {
            reset(vis2[i][j]);
            if (mp[i][j] == '1') continue;
            if (i == mid) setFlagTrue(vis2[i][j], j);
            else cpFlag(vis2[i][j], vis2[i - 1][j]);
            orFlag(vis2[i][j], vis2[i][j - 1]);
        }
    }
    vector<node> vl, vr;
    for (auto it: q) {
        if (it.x2 < mid) vl.push_back(it);
        else if (it.x1 > mid) vr.push_back(it);
        else ans[it.id] = andFlagAny(vis1[it.x1][it.y1], vis2[it.x2][it.y2]);
    }
    dfs(l, mid - 1, vl);
    dfs(mid + 1, r, vr);
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mp[i][j];
            if (mp[i][j] == '0') L[i][j] = L[i][j - 1] + 1;
        }
    }
    for (int j = 1; j <= m; j++) {
        for (int i = 1; i <= n; i++) {
            if (mp[i][j] == '0') U[i][j] = U[i - 1][j] + 1;
        }
    }

    int q;
    cin >> q;
    for (int i = 1; i <= q; i++) {
        int op, x1, x2, y1, y2;
        cin >> op >> x1 >> y1 >> x2 >> y2;
        if (x1 > x2 || y1 > y2) {
            ans[i] = 0;
            continue;
        }
        if (op == 1) {
            if (y1 != y2 || U[x2][y2] < x2 - x1) ans[i] = 0;
            else ans[i] = 1;
        } else if (op == 2) {
            if (x1 != x2 || L[x2][y2] < y2 - y1) ans[i] = 0;
            else ans[i] = 1;
        } else {
            queryList.push_back({i, x1, y1, x2, y2});
        }
    }
    dfs(1, n, queryList);

    for (int i = 1; i <= q; i++) cout << (ans[i] ? "yes\n" : "no\n");
}

当然，如果你了解 bitset 的话，那么就更好办了

ACM&算法

#ACM

2021年浙江工商大学新生赛题解

https://blog.mauve.icu/2021/11/21/acm/other-note/2021-ZJGSU-ACM-freshman-competition/

作者

Shiroha

发布于

2021年11月21日

许可协议

GitHub 下载的 zip 代码如何与原仓库再次建立连接上一篇

Dockerfile 中下载 JDK8 下一篇