Codeforces Round 897 (Div. 2)

A. green_gold_dog, array and permutation

大致题意

已知一个数组 $a$，长度为 $n$，需要给出一个 $n$ 的排列 $b$，使得得到的新数组 $c_i = a_i - b_i$ 中不同的值尽可能多，问数组 $b$ 的结果可能是

思路

简单来说就是要差值差异大，而且没有取 $abs$，所以可以直接排序一下，一个递增一个递减配对即可

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<pair<int, int>> data(n);
        for (auto &item: data) cin >> item.first;
        for (int i = 0; i < n; ++i) data[i].second = i;
        sort(data.begin(), data.end(), greater<>());
        for (int i = 0; i < n; ++i) data[i].first = i + 1;
        sort(data.begin(), data.end(), [](const pair<int, int> &lhs, const pair<int, int> &rhs) {
            return lhs.second < rhs.second;
        });
        for (int i = 0; i < n; ++i) cout << data[i].first << " \n"[i == n - 1];
    }
}

B. XOR Palindromes

大致题意

已经存在一个二进制的字符串 $a$，长度为 $n$，若存在另外一个字符串 $b$，其长度也为 $n$，其中 1 的数量恰好为 $x$，使得 $a \oplus b$ 恰好是一个回文串。则称 $x$ 是一个好值，问在 $[0, n]$ 中哪些值是好值

思路

首先，在异或操作中，若其中一方为 1 已知，那么相当于对对方进行了翻转操作。

而要回文串，那么必然可以将初始串先按位分割，只看左右的其中一半，若这个位置本来就会回文（和后半对应的位置相同），那么需要寻找的串必定这两位要相同，否则必须不同，由此可以计算出至少要 1 的数量和最多能够用上的 1 的数量。

另外关注字符串本身是否是奇数长度的，这样意味着如果恰好多一个，就可以放到中间解决问题，如果不是的话，那么满足条件的值会间隔开

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        string str;
        cin >> str;
        str.reserve(n);
        int diff = 0, same = 0;
        for (int i = 0; i < (n + 1) / 2; ++i) {
            diff += str[i] != str[n - 1 - i];
            same += str[i] == str[n - 1 - i];
        }
        for (int i = 0; i <= n; ++i) {
            if (i < diff || i > n - diff) cout << 0;
            else if (n % 2) cout << 1;
            else {
                if ((i - diff) % 2 == 0) cout << 1;
                else cout << 0;
            }
        }
        cout << endl;
    }
}

C. Salyg1n and the MEX Game

交互题（这场交互题真多）

大致题意

有一个初始的集合，里面有一些值，你可以每次往里面加一个不存在的值，然后机器会每次往里面删除一个存在的值，且每次删除的值一定比你加入的值小。如果无法删除值了（没有满足条件的值了）那么就结束，问如何使得 MEX 最大化

思路

实际上对于删除方，第一优先级的肯定是删除掉最小的值，因为只有这样能最有效的降低 MEX。

对于你而言，一旦试图添加 0 这种最低值的时候，游戏就会结束，此时 MEX 就取决于往后的第一个空档。可以发现一旦被删除掉的值是最小的，那么就再也不能救回比那个值更小的可能性了。而因为最终一次操作一定是加入的，所以只需要对方删除啥你就加入什么即可，保证不要被删掉小的值。而第一次加入，就可以选择当前的 MEX，来增加最终的 MEX 的结果

题非常简单易懂，但是解释起来又有些难

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> data(n);
        for (auto &item: data) cin >> item;
        sort(data.begin(), data.end());
        int mex = n;
        for (int i = 0; i < n; ++i)
            if (data[i] != i) {
                mex = i;
                break;
            }
        cout << mex << endl;
        cout.flush();
        while (cin >> mex && mex != -1) {
            cout << mex << endl;
            cout.flush();
        }
    }
}

D. Cyclic Operations

大致题意

有一个初始每一个值都是 0 的数组 $a$，长度为 $n$，希望变成目标数组 $b$，可以进行如下操作

• 构造任意一个长度恰好为 $k$ 的数组 $c$，$k$ 为给出的固定数字
• $\forall i \in [1, k], a_{l_i} \rightarrow l_{(i \space mod \space k) + 1}$

允许进行无数次操作，问是否有可能变成 $b$

思路

首先仔细模拟一下这个看起来很恐怖的公式，发现其实就是 $a_{l_i} \rightarrow l_{i+1}$ 注意这里可以看成是循环数组，否则会越界

然后考虑一下特殊情况，就是 $k = 1$ 的情况，这个时候必须每个值的下标等于自己，否则肯定不行，这里就不过多解释了，模拟一下就行。

然后是其他情况下，模拟一下就会发现有点类似有向图一样，而且比较显而易见必然会产生环

所以只需要让有向图上的环的大小都恰好等于 $k$ 即可，对于分支链路，他们可以直接临时占用环的一部分，而后通过环本身将其覆盖即可

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, k;
        cin >> n >> k;
        vector<int> data(n);
        vector<int> circle(n, 0);
        vector<int> level(n, 0);
        for (auto &item: data) cin >> item;
        if (k == 1) {
            bool flag = true;
            for (int i = 0; i < n; ++i) if (data[i] != i + 1) flag = false;
            cout << (flag ? "YES" : "NO") << endl;
            continue;
        }

        bool flag = true;
        int cur = 1;
        for (int i = 0; i < n; ++i) {
            if (circle[i] != 0) continue;
            cur++;
            int len = 0, index = i;
            while (circle[index] == 0) {
                circle[index] = cur;
                level[index] = len++;
                index = data[index] - 1;
            }
            if (circle[index] != cur) {
                // other circle, no matter how len it is, always OK
                continue;
            }
            if (len - level[index] != k) {
                flag = false;
                break;
            }
        }
        cout << (flag ? "YES" : "NO") << endl;
    }
}

E2. Salyg1n and Array (hard version)

easy version 要求更低，所以直接做 hard

大致题意

有一个未知的数组，长度为 $n$，需要求出整个数组的异或和是多少

每次可以询问一个区间的异或和，这个区间长度一定为给定的 $k$，询问后，整个区间将会翻转

最多只能请求 57 次

思路

很显然，可以知道至多 $50$ 就可以保证覆盖到所有的区间，如果恰好 $k$ 是 $n$ 的因子，那么就可以恰好满覆盖，循环一遍直接可以得到答案了

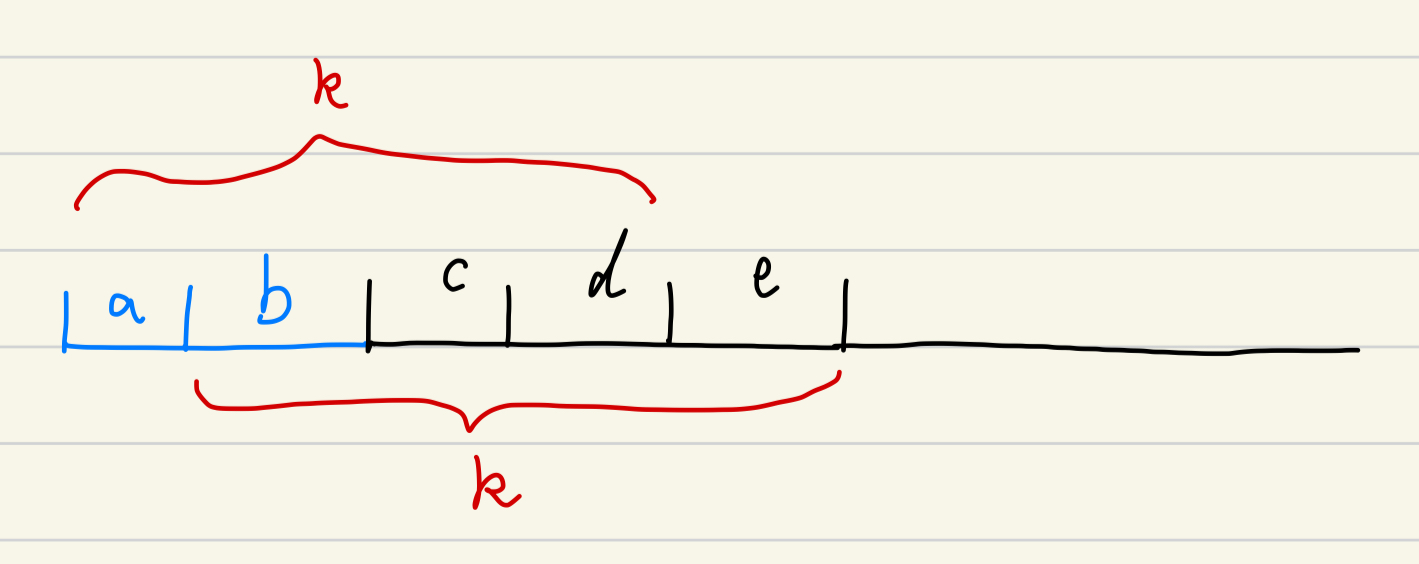
如果不满足的情况，就需要考虑一种方案了，这里给出我的一个方案，接下来会参考下面的图进行讲解，图中，$a, b$ 两段之和（蓝色部分）是不满足完美分配后，余下的部分，其他的黑色部分则是可以完美分配的部分，其中 $len(a) = len(b) = len(d) = len(e)$（注意题目中描述了 $n, k$ 必定都是偶数，所以肯定可以这样分配），同时 $len(a) + len(b) + len(c) + len(d) = k$，且 同时 $len(b) + len(c) + len(d) + len(e) = k$

先要求算出 $a,b,c,d$ 这个区间的异或和，假设记为 $x$，如此操作后，必定迎来翻转操作，即区间变成 $d, (c+b), a, e$ 的顺序，其中因为 $c$ 区间长度不确定，故和 $b$ 放在一块，不做区分。

然后再计算 $(c+b), a, e$ 的区间异或和，得到 $y$，同时翻转后得到 $d, e | (a+b+c)$，此处同理，此时无法完美区分 (a+b+c) 的区间长度到底是多少，只是大概知道个顺序罢了，因为我们也不关心顺序，故合并起来写，注意中间的其，其表示原来图中的蓝色和黑色部分的分割线。第一次翻转后，这根线无法进行绘制故没有标出，此时可以标出了

接着计算 $x \oplus y = (a \oplus b \oplus c \oplus d) \oplus (c \oplus b \oplus a \oplus e) = d \oplus e$，这不是正好是翻转后的外面部分的，那么问题好像就解决了

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, k, ans = 0, tmp;
        cin >> n >> k;
        if (n % k != 0) {
            int len = n % k;
            cout << "? 1" << endl;
            cout.flush();
            cin >> tmp;
            ans ^= tmp;
            cout << "? " << (len / 2 + 1) << endl;
            cout.flush();
            cin >> tmp;
            ans ^= tmp;
        }
        for (int i = n % k; i < n; i += k) {
            cout << "? " << i + 1 << endl;
            cout.flush();
            cin >> tmp;
            ans ^= tmp;
        }
        cout << "! " << ans << endl;
    }
}