Codeforces Round 909 (Div. 3)

A. Game with Integers

大致题意

有两个人 A/B 博弈，每次操作可以使一个值 $+1/-1$

问在 A 先操作的情况下，A 操作后恰好值可以被 3 整除，则 A 获胜，给出初始值，问 A 是否可能获胜

思路

初始是 3 的倍数就不能获胜，很简单

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        cout << (n % 3 ? "First" : "Second") << endl;
    }
}

B. 250 Thousand Tons of TNT

大致题意

有 $n$ 箱 TNT，不同重量但顺序固定，有 $k$ 辆卡车，每辆卡车从第一箱 TNT 开始取，每辆车恰好分到 $\frac{n}{k}$ 个 TNT 箱。

问在所有可能的 $k$ 下，什么时候可以使得最重的卡车和最轻的卡车差值最大。

(不过，题意中题到了 MrBeast，有意思)

思路

在可能的 $k$ 下，说明必须是 $n$ 的因子，因为一个数的因子不可能很多，所以暴力扫就行了

AC code

#define int long long

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> data(n);
        for (auto& i: data) cin >> i;

        auto cal = [&](const int x) {
            int mi = LONG_LONG_MAX, ma = 0;

            for (int i = 0; i < n; i += x) {
                int tmp = 0;
                for (int j = 0; j < x; ++j) tmp += data[i + j];
                mi = min(mi, tmp);
                ma = max(ma, tmp);
            }

            return ma - mi;
        };

        int ans = 0;
        for (int i = 1; i < n; ++i) {
            if (n % i) continue;
            ans = max(cal(i), ans);
        }
        cout << ans << endl;
    }
}

C. Yarik and Array

大致题意

类似最大的连续字串和，只不过还要求必须奇偶间隔开

思路

稍微改一下 dp 转移方程即可，非常简单

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> data(n);
        for (auto& i: data) cin >> i;
        vector<int> ans(n);
        ans[0] = data[0];
        int res = ans[0];
        for (int i = 1; i < n; ++i) {
            if (abs(data[i]) % 2 ^ abs(data[i - 1]) % 2) ans[i] = max(data[i], ans[i - 1] + data[i]);
            else ans[i] = data[i];
            res = max(res, ans[i]);
        }

        cout << res << endl;
    }
}

D. Yarik and Musical Notes

大致题意

有一个数组，问有多少个对满足 $(2^{b_i})^{2^{b_j}} = (2^{b_j})^{2^{b_i}}$

思路

$$\begin{cases} & (2^{b_i})^{2^{b_j}} & = & (2^{b_j})^{2^{b_i}} \\ \Rightarrow & 2^{b_i \times 2^{b_j}} & = & 2^{b_j \times 2^{b_i}} \\ \Rightarrow & b_i \times 2^{b_j} & = & b_j \times 2^{b_i} \\ \Rightarrow & \frac{b_i}{b_j} & = & \frac{2^{b_i}}{2^{b_j}} \\ \Rightarrow & \frac{b_i}{b_j} & = & 2^{b_i - b_j} \end{cases}$$

设 $x = b_i - b_j$，得 $b_i = x + b_j$

得到

$$\begin{cases} & \frac{b_j + x}{b_j} & = & 2^x \\ \Rightarrow & b_j + x & = & b_j \times 2^x \\ \Rightarrow & x & = & b_j \times (2^x - 1) \\ \Rightarrow & b_j & = & \frac{x}{2^x - 1} \\ \end{cases}$$

绘图可以得到

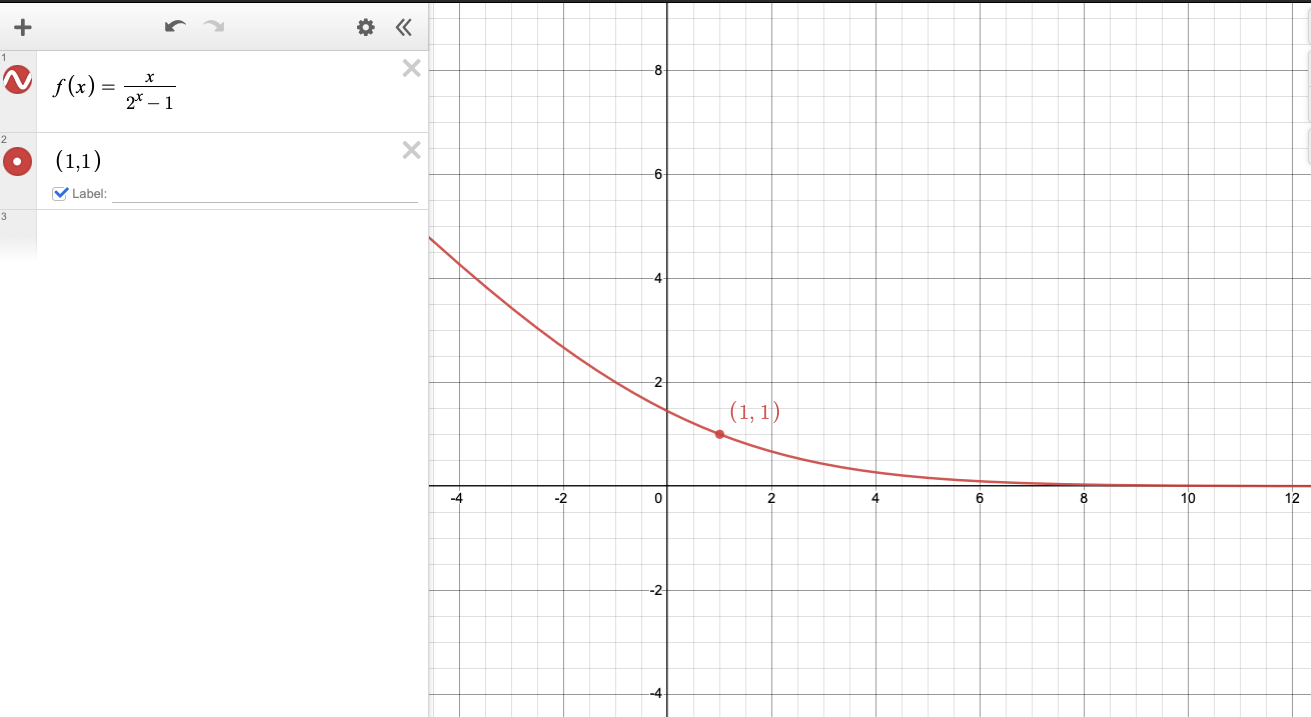
仅有 $x=0,x=1$ 有正整数解，所以显然，只能恰好相同或者恰好为 $1, 2$ 可以成对

AC code

#define int long long

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        map<int, int> cnt;
        for (int i = 0; i < n; ++i) {
            int tmp;
            cin >> tmp;
            ++cnt[tmp];
        }

        int ans = 0;
        for (auto [fst, snd]: cnt) ans += snd * (snd - 1) / 2;
        ans += cnt[1] * cnt[2];
        cout << ans << endl;
    }
}

E. Queue Sort

大致题意

每次可以把第一个值，从后往前找到第一个严格小于它的值，然后放到它后面，问操作几次可以让数组有序

思路

如果说当前值已经是最小的那个，那么每次移动一定会回到第一个，所以就会无法操作，即需要保证最小的那个出现的时候，后面的都得是有序的即可

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> data(n);
        for (auto& i: data) cin >> i;
        int mi = INT_MAX;
        for (const auto& i: data) mi = min(mi, i);
        int t = 0;
        while (data[t] != mi) ++t;
        bool flag = true;
        for (int i = t + 1; i < n; ++i) if (data[i] < data[i - 1]) flag = false;
        cout << (flag ? t : -1) << endl;
    }
}

F. Alex’s whims

大致题意

有一棵树，每次允许操作其中一条边（保证还是树的情况下）使得每次操作后，存在两个叶子节点（仅有一条边即为叶子节点）的距离恰好为给出的值

给出一种初始的树以及相关的操作方式

思路

简单题，都串成链，然后把最后的一个点，要多少，就连到哪，这样距离 $1$ 节点的距离恰好就是给出的值

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, q;
        cin >> n >> q;
        vector<int> data(q);
        for (auto& i: data) cin >> i;
        for (int i = 1; i < n; ++i) cout << i << ' ' << i + 1 << endl;
        int cur = n - 1;
        for (const auto& i: data) {
            if (i == cur) {
                cout << "-1 -1 -1" << endl;
                continue;
            }

            cout << n << ' ' << cur << ' ' << i << endl;
            cur = i;
        }
    }
}

G. Unusual Entertainment

大致题意

有一个 $n$ 的排列的数组 $p$，以及一棵节点数为 $n$ 的树，根为 $1$ 节点

每次询问 $l, r, x$，数组中 $[l, r]$ 区间内，是否存在至少一个点 $y$，满足 $y$ 是 $x$ 的一个孩子节点或者是 $x$ 本身

思路

我的思路和大部分人的思路不太一样，有一点比较暴力的味道。看起来这道题就要离线处理了，那么可以考虑在树上做一遍操作把所有答案都算出来

首先，如何找到一个节点全部的孩子节点，那么就可以考虑使用树上 dfs 的方式来查找，在进入 dfs 到离开 dfs 的期间，那么遇到的点都是它的孩子

如果说此时在遍历到某个节点 $n$，这个节点在上面的数组 $p$ 的位置是 $m$，且这个 $m$ 恰好出现在了它的父节点的某个询问中，即父节点询问的区间包含 $m$
那么这个父节点的这个询问就是成功的，命中的。

那么我们需要维护的就是这个节点上面所有的父节点的询问。由于询问都是区间的模式，那么可以考虑用线段树维护，每个线段树的节点保存所遇到的询问的集合。

当遍历到某个树上的节点 $n$ 的时候，找出它所在 $p$ 中的 $m$，然后再看看这个 $m$ 在哪些父节点的询问中，对遇到的询问都标记为有结果即可。

通过这个方式，在进入某个节点的时候，将对这个节点的询问都放进线段树，离开的时候，都从线段树里取走，就可以实现在树上 dfs 期间，通过线段树完成搜索

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, q;
        cin >> n >> q;
        struct node {
            int v, n;
        };
        vector<node> edge(n * 2 - 2);
        vector<int> head(n + 1, -1), pos(n + 1);;
        vector<vector<tuple<int, int, int>>> query(n + 1);
        vector<pair<int, int>> qs;
        for (int i = 0; i < n - 1; ++i) {
            int u, v;
            cin >> u >> v;
            edge[i << 1] = {v, head[u]};
            edge[i << 1 | 1] = {u, head[v]};
            head[u] = i << 1;
            head[v] = i << 1 | 1;
        }
        for (int i = 1; i <= n; ++i) {
            int tmp;
            cin >> tmp;
            pos[tmp] = i;
        }
        for (int i = 0; i < q; ++i) {
            int l, r, x;
            cin >> l >> r >> x;
            qs.emplace_back(l, r);
            query[x].emplace_back(l, r, i);
        }

        vector<set<int>> tree(n * 2 + 10);
        auto get = [](const int l, const int r) {
            return (l + r) | (l != r);
        };
        function<void(int, int, int, int, int)> _add = [&](const int l, const int r, const int x, const int y, const int v) {
            const int mid = l + r >> 1;
            if (x == l && y == r) {
                tree[get(l, r)].insert(v);
                return;
            }

            if (y <= mid) _add(l, mid, x, y, v);
            else if (x > mid) _add(mid + 1, r, x, y, v);
            else {
                _add(l, mid, x, mid, v);
                _add(mid + 1, r, mid + 1, y, v);
            }
        };
        function<bool(int, int, int, int, int)> _del = [&](const int l, const int r, const int x, const int y, const int v) {
            const int mid = l + r >> 1;
            if (x == l && y == r) {
                return tree[get(l, r)].erase(v) ? true : false;
            }

            if (y <= mid) return _del(l, mid, x, y, v);
            if (x > mid) return _del(mid + 1, r, x, y, v);
            return _del(l, mid, x, mid, v) && _del(mid + 1, r, mid + 1, y, v);
        };
        function<void(int, int, int, vector<int>&)> _find = [&](const int l, const int r, const int v, vector<int>& res) {
            for (const auto& i: tree[get(l, r)]) res.push_back(i);
            if (l == r) return;

            if (const int mid = l + r >> 1; v <= mid) {
                _find(l, mid, v, res);
            } else if (v > mid) {
                _find(mid + 1, r, v, res);
            }
        };

        vector ans(q, false);
        vector<int> res;
        res.reserve(n);

        function<void(int, int)> dfs = [&](const int u, const int p) {
            for (const auto [l, r, i]: query[u]) _add(1, n, l, r, i);
            _find(1, n, pos[u], res);
            for (const auto& i: res) {
                ans[i] = true;
                _del(1, n, qs[i].first, qs[i].second, i);
            }
            res.clear();

            for (int i = head[u]; ~i; i = edge[i].n) {
                if (edge[i].v == p) continue;
                dfs(edge[i].v, u);
            }

            for (const auto [l, r, i]: query[u]) if (_del(1, n, l, r, i)) ans[i] = false;
        };

        dfs(1, 0);

        for (const auto& i: ans) cout << (i ? "YES" : "NO") << endl;
        cout << endl;
    }
}

ACM&算法

#ACM #Codeforces

Codeforces Round 909 (Div. 3)

https://blog.mauve.icu/2024/01/07/acm/codeforces/CodeforcesRound909/

作者

Shiroha

发布于

2024年1月7日

许可协议

Codeforces Round 910 (Div. 2) 上一篇

Codeforces Round 908 (Div. 2) 下一篇