Codeforces Round 910 (Div. 2)

A. Milica and String

大致题意

有一个 A/B 组成的字符串，每次允许选择前 $n$ 个字母，将他们都变成 A/B，问最少的操作次数

思路

简单题，最简单的方式就是枚举每一种可能，计算结果是否符合预期就行

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, k;
        cin >> n >> k;
        string str;
        str.reserve(n);
        cin >> str;
        int cntB = 0;
        for (int i = 0; i < n; ++i) cntB += str[i] == 'B';
        if (cntB == k) {
            cout << 0 << endl;
            continue;
        }

        const bool useA = cntB > k;
        for (int i = 0; i < n; ++i) {
            if (cntB > k) {
                cntB -= str[i] == 'B';
            } else {
                cntB += str[i] != 'B';
            }

            if (cntB == k) {
                cout << 1 << endl;
                cout << i + 1 << ' ' << (useA ? 'A' : 'B') << endl;
                break;
            }
        }
    }
}

B. Milena and Admirer

大致题意

允许不断的差分一个数组中的值，问至少需要拆多少次，才能让数组非递减

思路

也比较简单，从后往前遍历，如果当前值比后面的值大，则均匀的拆成 $x$ 份，使得恰好比后面的值小或者相同即可

AC code

#define int long long

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> data(n);
        for (auto& i: data) cin >> i;
        int ans = 0;
        for (int i = n - 2; i >= 0; --i) {
            if (data[i] > data[i + 1]) {
                const int cut = data[i] / data[i + 1] + (data[i] % data[i + 1] == 0 ? 0 : 1);
                data[i] /= cut;
                ans += cut - 1;
            }
        }
        cout << ans << endl;
    }
}

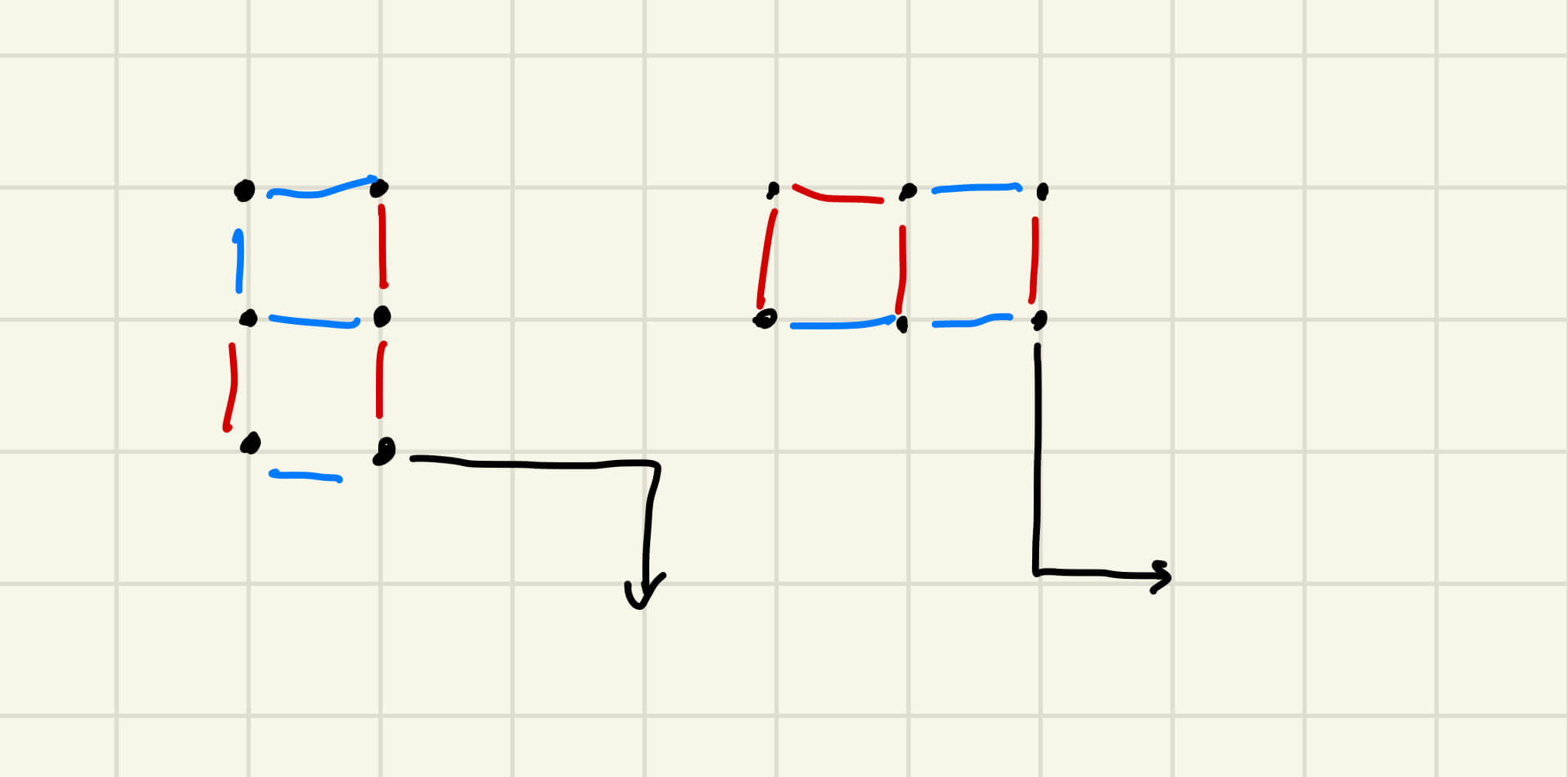
C. Colorful Grid

大致题意

有一个棋盘，允许在棋盘的边上染色，然后使得从最左上角到最右下角的某一条路径长度恰好为 $k$ 的同时，路径上一定上红蓝间隔染色的

思路

即然可以重复点，那么最好的办法是找一个可以旋转的环，在里面转到足够多次就行。

因为需要红蓝间隔，那么必然最小的环就是 $4$ 个单位长度的格子，所以如果 $k$ 恰好是最短的距离加上 $4n$ 的话，就可以这样解决

但是还有一种情况，也就是不满足 $4n$ 的时候，例如 $3 \times 2$ 的方格，走 5 步，也是可以到达的（可以自己绘制一下）

故所以需要兼容上面的两种情况，我给出的一种解法如下

首先根据矩形的长边，旋选择左边或者右边的，然后固定将左上角绘制成上述形状，然后再补充移动到右下角的路径即可

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, m, k;
        cin >> n >> m >> k;
        const int mi = n - 1 + m - 1;
        if (k < mi) {
            cout << "NO" << endl;
            continue;
        }

        if (const int cut = k - mi; cut != 0 && cut % 2 == 1) {
            cout << "NO" << endl;
            continue;
        }

        if (n == 2 && m == 2) {
            if (k % 4 != 2) cout << "NO" << endl;
            else cout << "B\nB\nR R" << endl;
            continue;
        }

        vector<vector<char>> a(n), b(n - 1);
        for (auto& i: a) i.resize(m - 1);
        for (auto& i: b) i.resize(m);

        if (n >= m) {
            a[0][0] = a[1][0] = a[2][0] = b[0][0] = 'B';
            b[0][1] = b[1][0] = b[1][1] = 'R';
            for (int i = 1; i < m - 1; ++i) a[2][i] = a[2][i - 1] == 'R' ? 'B' : 'R';
            const char last = b[1][m - 1];
            b[1][m - 1] = a[2][m - 2];
            for (int i = 2; i < n - 1; ++i) b[i][m - 1] = b[i - 1][m - 1] == 'R' ? 'B' : 'R';
            b[1][m - 1] = last;
        } else {
            a[0][0] = b[0][0] = b[0][1] = b[0][2] = 'R';
            a[0][1] = a[1][0] = a[1][1] = 'B';
            for (int i = 1; i < n - 1; ++i) b[i][2] = b[i - 1][2] == 'R' ? 'B' : 'R';
            const char last = a[n - 1][1];
            a[n - 1][1] = b[n - 2][2];
            for (int i = 2; i < m - 1; ++i) a[n - 1][i] = a[n - 1][i - 1] == 'R' ? 'B' : 'R';
            a[n - 1][1] = last;
        }
        cout << "YES" << endl;
        for (const auto& i: a) {
            for (const auto& j: i) cout << (j ? j : 'R') << ' ';
            cout << endl;
        }
        for (const auto& i: b) {
            for (const auto& j: i) cout << (j ? j : 'R') << ' ';
            cout << endl;
        }
    }
}

D. Absolute Beauty

大致题意

有两个数组，允许交换 $b$ 数组中的两个值一次，问使得 $\sum^n_{i=1} \left | a_i - b_i \right |$ 最大的可能是多少

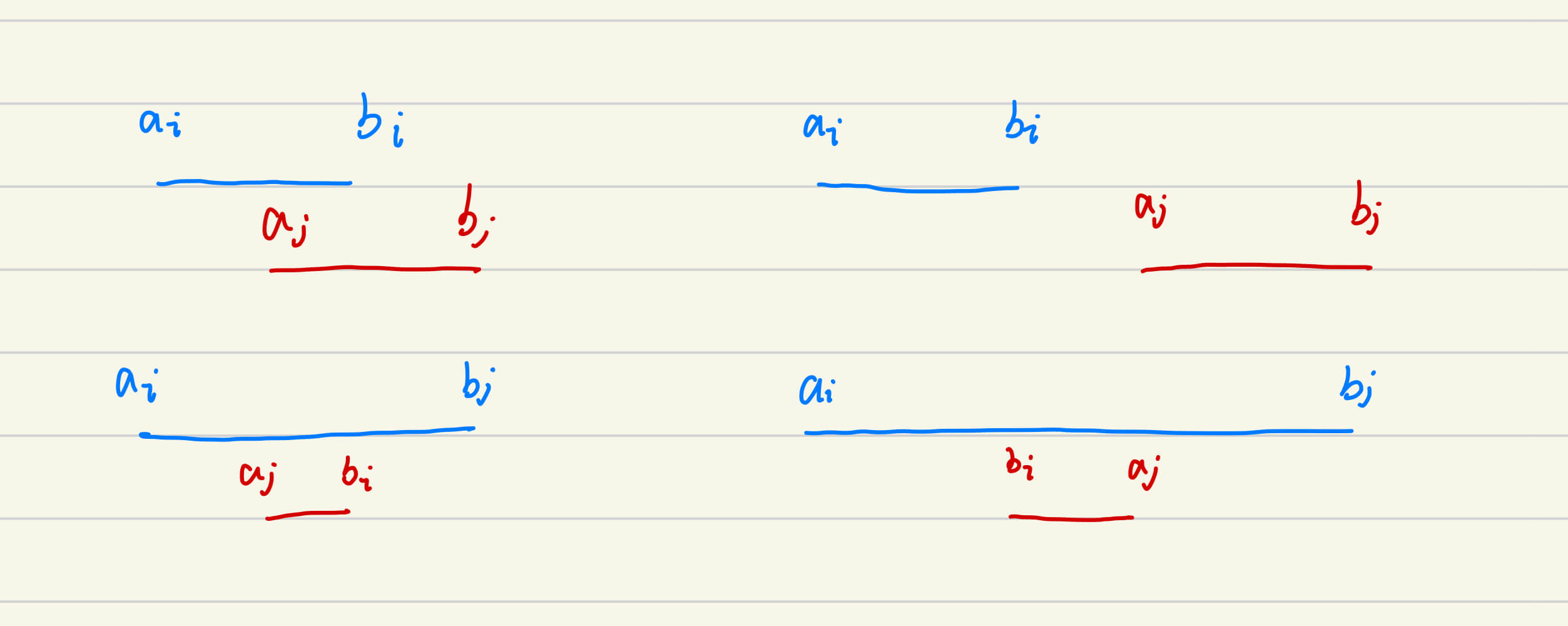
思路

首先得画几个图来理解，为了方便，此处先假定 $a_i < b_i$（后续可以证明可以恒定满足此等式）

那么可以得到主要有两种情况

可见，只有右边的情况是能够真正有意义的，有意义的部分是 $a_j - b_i$

那么就需要找到最大的 $a_j - b_i$ 即可

然后我们再来看看如何证明最开始说的 $a_i < b_i$。你可以尝试将图里的 $a,b$ 交换位置，你会发现对最终的结果没有影响

AC code

#define int long long

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n;
        cin >> n;
        vector<int> a(n), b(n);
        for (auto& i: a) cin >> i;
        for (auto& i: b) cin >> i;
        for (int i = 0; i < n; ++i) if (a[i] > b[i]) swap(a[i], b[i]);

        int mib = 0, maa = 0;
        for (int i = 0; i < n; ++i) {
            if (b[i] < b[mib]) mib = i;
            if (a[i] > a[maa]) maa = i;
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) ans += abs(a[i] - b[i]);
        ans += max(0LL, 2 * (a[maa] - b[mib]));
        cout << ans << endl;
    }
}

E. Sofia and Strings

大致题意

有一个字符串 $a$，允许你无数次操作如下的两个方法其中之一

• 选择其中一个片段，进行排序
• 删掉一个指定的字符

问是否能够变成 $b$ 字符串

思路

这里的选择片段排序，实际上最有用的就是选择两个相邻的字母排序，这样就可以最小的改动的情况下，将一个值往前移动

而需要达成这个目标，就意味着每次移动的时候，前面的值都需要比当前值大，否则前面的值只能删除。

故可以考虑遍历 $b$ 的字母，找到当前可用的最小的在 $a$ 中的位置，并将前面的那些字符移动到后面（比当前字母大），或者删除

AC code

void solve() {
    int _;
    cin >> _;
    for (int ts = 0; ts < _; ++ts) {
        int n, m;
        cin >> n >> m;
        string sn, sm;
        sn.reserve(n);
        sm.reserve(m);
        cin >> sn >> sm;
        vector<queue<int>> v(26);
        for (int i = 0; i < n; ++i) v[sn[i] - 'a'].push(i);

        bool flag = true;
        for (int i = 0; i < m; ++i) {
            if (v[sm[i] - 'a'].empty()) {
                flag = false;
                break;
            }

            int t = v[sm[i] - 'a'].front();
            v[sm[i] - 'a'].pop();

            for (int j = 0; j < sm[i] - 'a'; ++j) while (!v[j].empty() && v[j].front() < t) v[j].pop();
        }

        cout << (flag ? "YES" : "NO") << endl;
    }
}